Phân phối Poisson là một trong những nội dung quan trọng nhất của môn học xác suất thống kê. Đồng thời, đây được coi là nội dung khá khó để tiếp cận đối với nhiều người. Bài viết dưới đây chúng tôi sẽ cung cấp cho bạn đầy đủ kiến thức về phân phối Poisson.
Phân phối Poisson là gì?
Phân phối Poisson (Tiếng Anh: Poisson distribution) là một phân phối xác suất rời rạc mô tả số lần xuất hiện của một sự kiện ngẫu nhiên trong một khoảng thời gian hoặc không gian nhất định, với giả định rằng các sự kiện này xảy ra độc lập với nhau và với tỷ lệ trung bình không đổi theo thời gian hoặc không gian.
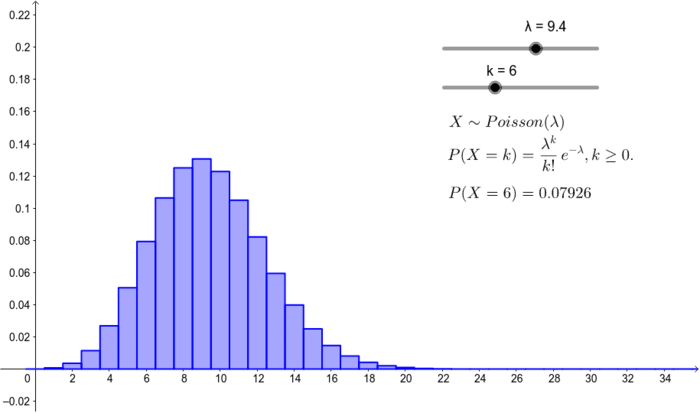
Đặc trưng của phân phối này là nó chỉ phụ thuộc vào một tham số duy nhất, thường được ký hiệu là λ (lambda), đại diện cho số lần trung bình mà sự kiện xảy ra trong khoảng thời gian hoặc không gian đã cho. Phân bố Poisson thường được áp dụng trong các tình huống như đếm số cuộc gọi đến tổng đài trong một giờ, số lỗi in trong một trang sách, hay số hạt phóng xạ phân rã trong một khoảng thời gian nhất định. Một đặc điểm đáng chú ý của phân phối này là kỳ vọng và phương sai của nó bằng nhau và bằng tham số λ.
Công thức của phân phối Poisson
Công thức đầy đủ của Poisson distribution là gì và ví dụ minh họa sẽ được chúng tôi cung cấp đầy đủ dưới đây.
Công thức phân phối Poisson
Công thức xác suất của phân phối Poisson hay Poisson Distribution cho biết xác suất xảy ra k sự kiện trong một khoảng thời gian hoặc không gian nhất định, với tỷ lệ trung bình λ, được biểu thị như sau:
P(X = k) = (e^(-λ) * λ^k) / k!
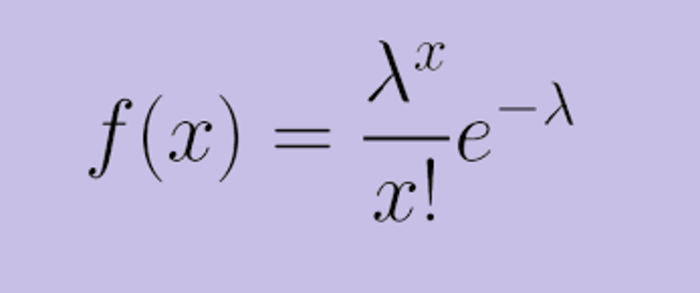
Giải thích ký hiệu công thức như sau:
- P(X = k): Xác suất xảy ra k sự kiện.
- k: Số lần xuất hiện của sự kiện, là một giá trị rời rạc không âm (k = 0, 1, 2, 3, …).
- λ: Tỷ lệ trung bình của sự kiện xảy ra, là một giá trị dương (λ > 0).
- e: Số Euler, xấp xỉ bằng 2.71828.
- k!: Khai triển giai thừa của k, là tích của các số nguyên dương từ 1 đến k (k! = 1 * 2 * 3 * … * k).
Ví dụ minh họa
Giả sử bạn muốn tính xác suất có 2 sự kiện xảy ra trong 1 giờ, với tỷ lệ trung bình 0.5 sự kiện mỗi 30 phút (λ = 0.5/0.5 = 1 sự kiện/giờ). Sử dụng công thức Poisson Distribution, ta có: P(X = 2) = (e^(-1) * 1^2) / 2! ≈ 0.135
Vậy, xác suất có 2 sự kiện xảy ra trong 1 giờ là khoảng 13.5%.
Cách đặc trưng của phân phối Poisson
Phân bố Poisson có những đặc trưng quan trọng như sau:
Giá trị kỳ vọng trung bình
Kỳ vọng (Expected Value) của Poisson distribution bằng chính tham số λ của nó. Điều này có nghĩa là giá trị trung bình của số lần sự kiện xảy ra trong khoảng thời gian hoặc không gian đã cho chính là λ. Đây là một đặc trưng quan trọng vì nó cho phép chúng ta ước lượng tham số λ từ dữ liệu quan sát được, đồng thời cũng giúp dự đoán số lần sự kiện có thể xảy ra trong tương lai dựa trên thông tin về tốc độ trung bình.
Phương sai
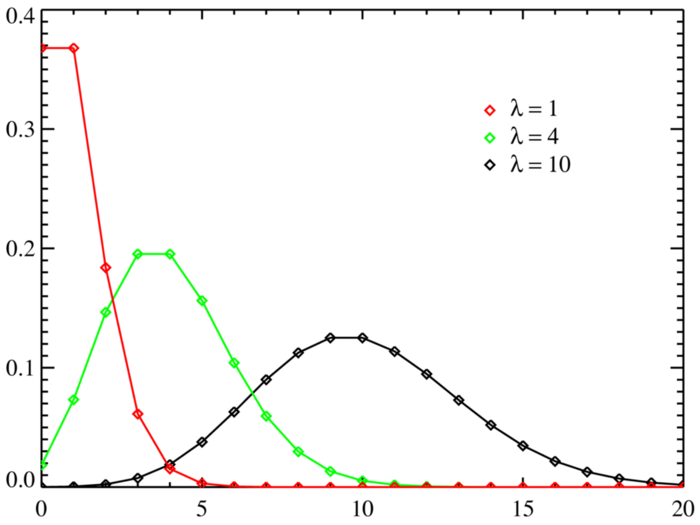
Phương sai (Variance) của phân phối Poisson cũng bằng tham số λ. Đây là một đặc điểm độc đáo của phân phối này, khi mà kỳ vọng và phương sai có cùng giá trị. Phương sai cho biết mức độ phân tán của các giá trị xung quanh giá trị trung bình. Trong trường hợp của Poisson distribution, điều này ngụ ý rằng khi λ tăng lên, không chỉ số lần sự kiện xảy ra trung bình tăng mà độ biến động của số lần xảy ra cũng tăng theo.
Hàm sinh moment
Hàm sinh moment (Moment Generating Function) của phân phối Poisson là M(t) = e^(λ(e^t – 1)). Hàm này rất hữu ích trong việc tính toán các moment của phân phối, cũng như trong việc chứng minh các tính chất quan trọng khác. Thông qua hàm sinh moment, ta có thể dễ dàng tính được các moment bậc cao hơn của Poisson distribution khi cần thiết.
Tính chất cộng tính
Tính chất cộng tính (Additive Property) là một đặc trưng quan trọng khác của phân bố Poisson. Nếu X và Y là hai biến ngẫu nhiên độc lập tuân theo phân bố Poisson với các tham số lần lượt là λ1 và λ2, thì tổng X + Y cũng tuân theo phân phối Poisson với tham số λ1 + λ2. Tính chất này rất hữu ích trong việc mô hình hóa các hệ thống phức tạp, nơi nhiều sự kiện độc lập cùng xảy ra.
Một vài lưu ý về phân phối Poisson
Khi tìm hiểu và nghiên cứu về phân bố Poisson bạn cần lưu ý một vài điều sau đây:
- Phân phối Poisson chỉ áp dụng cho các biến ngẫu nhiên rời rạc, nghĩa là các giá trị của biến chỉ có thể là các số nguyên không âm.
- Các sự kiện xảy ra theo phân bố Poisson phải độc lập với nhau và có tỷ lệ trung bình không đổi theo thời gian hoặc không gian.
- Nếu các giả định này không được đáp ứng, thì việc sử dụng công thức phân bố Poisson có thể dẫn đến kết quả không chính xác.
Bên cạnh đó, ngoài công thức xác suất điểm (P(X = k)), Poisson distribution còn có các công thức khác như:
- Công thức xác suất tích lũy: P(X ≤ k) = Σ(j=0)^k P(X = j)
- Công thức hàm mật độ xác suất: f(x) = (e^(-λ) * λ^x) / x! (x = 0, 1, 2, …)
- Công thức giá trị kỳ vọng: E(X) = λ
- Công thức phương sai: Var(X) = λ
Lời kết
Tổng kết, bài viết trên chúng tôi đã cung cấp đầy đủ kiến thức về phân phối Poisson. Chúng tôi hy vọng rằng thông tin chúng tôi cung cấp có ý cho quá trình học tập nghiên cứu của bạn về nội dung này.




