Kiến thức cơ bản về phân số là gì và ứng dụng trong toán lớp 4

Phân số là gì? Đây là một trong những khái niệm cơ bản trong toán học, giúp chúng ta hiểu và tính toán các tỉ lệ. Trong bài viết này, bạn sẽ tìm thấy những kiến thức thú vị về phân số, từ cách biểu diễn cho đến phương pháp tối giản và ứng dụng trong thực tế. Hãy cùng khám phá và làm quen với các phép tính cơ bản liên quan đến phân số!

Phân số là gì?

Phân số là cách biểu diễn một số được tạo thành bởi hai phần: tử số và mẫu số, trong đó mẫu số khác 0. Tử số nằm phía trên và mẫu số nằm phía dưới, được ngăn cách bởi một dấu gạch ngang nằm ngang. Phân số trong toán học thể hiện phép chia của tử số cho mẫu số.

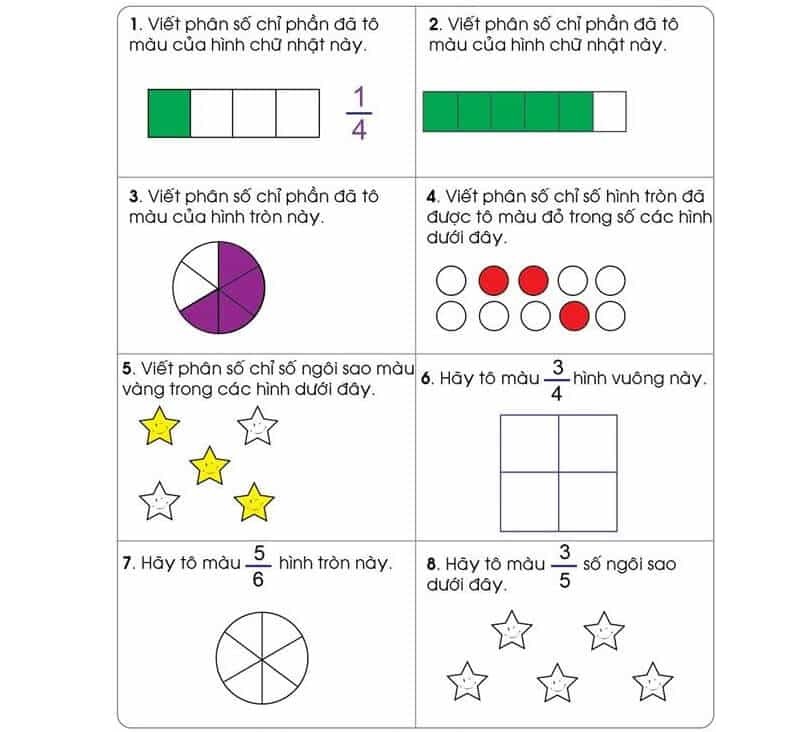
Khi học về phân số là gì, ta cần hiểu rằng đây là một khái niệm toán học cơ bản dùng để biểu diễn một phần của một đơn vị hoàn chỉnh. Ví dụ, khi chia một chiếc bánh thành 4 phần bằng nhau và lấy 3 phần, ta có thể biểu diễn số lượng đã lấy bằng phân số 3/4. Trong đó, 3 là tử số (số phần đã lấy) và 4 là mẫu số (tổng số phần được chia).

Phân số có thể được sử dụng để biểu diễn nhiều loại số khác nhau. Một số nguyên có thể được viết dưới dạng phân số bằng cách đặt mẫu số là 1. Số thập phân tuần hoàn cũng có thể được chuyển đổi thành phân số. Điều này giúp việc tính toán trở nên chính xác và dễ dàng hơn trong nhiều trường hợp.

Các thành phần cơ bản và cách biểu diễn phân số trong toán học

Phân số trong toán học là cách biểu diễn một số bằng tỷ số giữa hai số nguyên, trong đó số bị chia gọi là tử số và số chia gọi là mẫu số. Phân số là gì có thể hiểu đơn giản là một cách thể hiện phép chia giữa hai số nguyên, giúp biểu diễn chính xác các giá trị không thể biểu diễn bằng số nguyên.

Tử số và mẫu số trong phân số

Tử số là số nằm phía trên của phân số, thể hiện số phần được lấy ra từ tổng số phần bằng nhau. Ví dụ trong phân số 3/4, số 3 là tử số cho biết ta lấy 3 phần.

Mẫu số là số nằm phía dưới của phân số, cho biết tổng số phần bằng nhau mà một đơn vị được chia ra. Trong phân số 3/4, số 4 là mẫu số thể hiện một đơn vị được chia thành 4 phần bằng nhau.

Các dạng biểu diễn phân số thường gặp

Phân số có thể được biểu diễn dưới nhiều dạng khác nhau tùy theo mục đích sử dụng. Phân số tối giản là dạng phân số có tử số và mẫu số không còn ước chung lớn hơn 1, như 1/2 không thể rút gọn được nữa.

Phân số thường được viết dưới dạng a/b hoặc $frac{a}{b}$ trong toán học. Ngoài ra còn có dạng phân số hỗn hợp, bao gồm một số nguyên và một phân số như 1$frac{1}{2}$ (một và một phần hai).

Mối quan hệ giữa phân số và số thập phân

Phân số có thể chuyển đổi thành số thập phân hữu hạn là gì bằng cách thực hiện phép chia tử số cho mẫu số. Ví dụ phân số 1/2 = 0,5 hay 3/4 = 0,75.

Không phải mọi phân số đều cho kết quả là số thập phân hữu hạn. Một số phân số khi chia sẽ cho số thập phân vô hạn tuần hoàn như 1/3 = 0,333… Điều này phụ thuộc vào mẫu số của phân số sau khi tối giản có chứa các thừa số nguyên tố khác 2 và 5 hay không.

Phân số tối giản và cách tìm phân số tối giản

Phân số tối giản là gì – đây là dạng phân số có tử số và mẫu số không thể rút gọn được nữa bằng cách chia cho ước chung lớn nhất của chúng. Phân số tối giản giúp biểu diễn một giá trị phân số theo cách đơn giản và chính xác nhất.

Khái niệm phân số tối giản

Một phân số tối giản được định nghĩa là phân số có tử số và mẫu số nguyên tố cùng nhau, nghĩa là ước chung lớn nhất của tử số và mẫu số bằng 1. Ví dụ phân số 2/3 là phân số tối giản vì 2 và 3 không có ước chung nào lớn hơn 1.

Phân số tối giản có vai trò quan trọng trong toán học và các ứng dụng thực tế. Nó giúp biểu diễn các phép tính phân số một cách gọn gàng, dễ hiểu và chính xác hơn. Trong kinh doanh, phân số tối giản thường được sử dụng để thể hiện tỷ lệ phần trăm hay tỷ suất lợi nhuận một cách đơn giản nhất.

Các bước rút gọn phân số về dạng tối giản

Để rút gọn một phân số về dạng tối giản, ta thực hiện theo trình tự:

Bước 1: Tìm ước chung lớn nhất của tử số và mẫu số
Bước 2: Chia cả tử số và mẫu số cho ước chung lớn nhất vừa tìm được
Bước 3: Kết quả thu được là phân số tối giản

Ví dụ với phân số 12/18:

• Tìm ƯCLN của 12 và 18 = 6
• Chia cả tử và mẫu cho 6: 12÷6/18÷6 = 2/3

Vậy 2/3 là dạng tối giản của phân số 12/18.

Ứng dụng ước số chung lớn nhất để tối giản phân số

Để tối giản phân số hiệu quả, việc nắm vững khái niệm ước số là gì là rất quan trọng. Phương pháp tìm ước chung lớn nhất phổ biến nhất là phương pháp phân tích thừa số nguyên tố.

Khi áp dụng vào thực tế, ta có thể sử dụng các thuật toán như thuật toán Euclid để tìm ƯCLN nhanh chóng. Với các phân số đơn giản, có thể quan sát và rút gọn trực tiếp bằng cách chia cả tử và mẫu cho ước chung lớn nhất có thể thấy được.

Việc thành thạo kỹ năng tối giản phân số giúp đơn giản hóa các phép tính phức tạp và tránh sai sót trong quá trình giải toán. Đây là kỹ năng cơ bản cần thiết cho việc học tập môn toán ở các cấp cao hơn.

Phương pháp so sánh và quy đồng phân số

So sánh phân số là một kỹ năng toán học quan trọng giúp xác định giá trị tương đối giữa các phân số. Để thực hiện việc so sánh chính xác, cần nắm vững hai phương pháp chính là so sánh phân số cùng mẫu số và quy đồng mẫu số các phân số.

Việc so sánh và quy đồng phân số có vai trò thiết yếu trong nhiều bài toán thực tế như chia tỷ lệ, tính toán phần trăm hay phân chia tài sản. Để thực hiện được điều này, trước tiên cần hiểu rõ các nguyên tắc cơ bản.

Nguyên tắc so sánh phân số cùng mẫu số

Khi so sánh các phân số có cùng mẫu số, ta chỉ cần so sánh trực tiếp các tử số với nhau. Phân số nào có tử số lớn hơn sẽ là phân số lớn hơn, do chúng đang chia cho cùng một số.

Ví dụ, khi so sánh 3/7 và 5/7, ta thấy ngay 5/7 lớn hơn 3/7 vì 5 > 3. Điều này tương tự như việc chia một chiếc bánh thành 7 phần bằng nhau, lấy 5 phần sẽ nhiều hơn lấy 3 phần.

Cách quy đồng phân số

Cách quy đồng phân số là quá trình chuyển đổi các phân số về cùng mẫu số để dễ dàng so sánh. Đầu tiên, ta cần tìm bội chung nhỏ nhất (BCNN) của các mẫu số. Sau đó nhân cả tử và mẫu của mỗi phân số với một số thích hợp để được mẫu số mới bằng BCNN.

Để thực hiện chính xác, có thể tham khảo công thức tính phân số để nắm vững các bước tính toán. Việc quy đồng mẫu số giúp chuyển đổi các phân số về dạng tương đương nhưng có cùng mẫu số, từ đó dễ dàng so sánh.

Tìm phân số lớn nhất trong dãy phân số

Để tìm phân số lớn nhất trong một dãy phân số, cần quy đồng tất cả các phân số về cùng mẫu số. Sau khi quy đồng, ta chỉ cần so sánh các tử số và chọn phân số có tử số lớn nhất.

Một phương pháp khác là chuyển các phân số về số thập phân bằng cách chia tử số cho mẫu số. Cách này đặc biệt hữu ích khi cần so sánh nhiều phân số cùng lúc hoặc khi việc quy đồng mẫu số trở nên phức tạp.

Trong thực tế, các chuyên gia toán học thường kết hợp cả hai phương pháp tùy theo tình huống cụ thể để tìm ra cách giải quyết tối ưu nhất.

Các phép tính cơ bản với phân số trong chương trình toán lớp 4

Chương trình toán phân số lớp 4 tập trung vào việc rèn luyện 4 phép tính cơ bản: cộng, trừ, nhân và chia. Đây là nền tảng quan trọng giúp học sinh nắm vững kiến thức về phân số và áp dụng vào giải quyết các bài toán thực tế.

Việc thực hiện các phép tính với phân số lớp 4 đòi hỏi học sinh phải hiểu rõ quy tắc và thực hành nhiều để thành thạo. Tương tự như phép tính với số tự nhiên và lũy thừa, các phép tính với phân số cũng tuân theo những quy tắc nhất định.

Phép cộng và trừ phân số

Khi thực hiện phép cộng hoặc trừ phân số, bước đầu tiên là quy đồng mẫu số các phân số. Mẫu số chung thường được chọn là bội chung nhỏ nhất của các mẫu số ban đầu.

Sau khi quy đồng mẫu số, ta thực hiện phép cộng hoặc trừ các tử số với nhau và giữ nguyên mẫu số chung. Kết quả thu được cần được tối giản nếu có thể bằng cách chia cả tử số và mẫu số cho ước chung lớn nhất của chúng.

Phép nhân và chia phân số

Phép nhân phân số được thực hiện bằng cách nhân riêng tử số với tử số, mẫu số với mẫu số. Đây là phép tính đơn giản nhất trong cách tính phân số vì không cần quy đồng mẫu số.

Với phép chia phân số, ta chuyển về phép nhân bằng cách nhân với phân số nghịch đảo của số chia. Điều quan trọng là phải kiểm tra số chia khác 0 và tối giản kết quả sau khi thực hiện phép tính.

Bài tập vận dụng về phân số

Bài tập về phân số thường gắn liền với các tình huống thực tế như chia bánh, đo lường, tính toán thời gian. Ví dụ: Nam có 3/4 bánh pizza, Nam cho bạn 1/4 bánh. Hỏi Nam còn lại bao nhiêu bánh?

Giải quyết bài toán phân số cần tuân theo các bước: xác định phép tính cần dùng, kiểm tra mẫu số, thực hiện tính toán và rút gọn kết quả. Việc thực hành nhiều bài tập sẽ giúp học sinh thành thạo và tự tin hơn trong việc áp dụng kiến thức.

Ứng dụng của phân số trong thực tiễn và toán học nâng cao

Ứng dụng của phân số xuất hiện trong nhiều lĩnh vực của cuộc sống và toán học. Từ việc tính toán đơn giản trong sinh hoạt hàng ngày đến những bài toán phức tạp trong khoa học kỹ thuật, phân số đóng vai trò quan trọng giúp biểu diễn chính xác các đại lượng và mối quan hệ toán học.

Phân số trong đời sống hàng ngày

Trong nấu ăn, công thức thường yêu cầu đo lường nguyên liệu bằng phân số như 1/2 thìa đường hay 3/4 cốc bột. Theo khảo sát của Hiệp hội Đầu bếp Mỹ, 85% công thức nấu ăn sử dụng phân số để đảm bảo độ chính xác.

Trong xây dựng, thợ mộc sử dụng phân số để đo và cắt vật liệu chính xác. Ví dụ, một tấm gỗ dài 8 1/4 inch cần được cắt thành các phần bằng nhau 2 3/4 inch.

Trong tài chính cá nhân, phân số giúp tính toán lãi suất, chiết khấu và phân chia chi phí. Chẳng hạn như tính 1/3 thu nhập hàng tháng để trả góp khoản vay.

Phân số trong các bài toán phức tạp

Phân số đóng vai trò then chốt trong giải đạo hàm phân thức và tích phân. Trong đại số tuyến tính, phân số xuất hiện khi giải hệ phương trình và tính định thức ma trận.

Trong vật lý, phân số được dùng để biểu diễn các đại lượng như vận tốc, gia tốc và lực. Giáo sư Stephen Hawking từng nhấn mạnh tầm quan trọng của phân số trong việc mô tả các định luật vũ trụ.

Phân số là gì và cách vận dụng nó trong toán học nâng cao được giảng dạy chi tiết tại Học Thế Nào, giúp học sinh nắm vững kiến thức cơ bản trước khi đi sâu vào các ứng dụng phức tạp.

Mối liên hệ giữa phân số và số phức

Số phức là gì có mối liên hệ mật thiết với phân số thông qua phép chia và biểu diễn dạng lượng giác. Khi thực hiện phép chia số phức, ta cần nhân cả tử và mẫu với số phức liên hợp để được kết quả dưới dạng phân số.

Trong lý thuyết hàm phức, phân số giúp biểu diễn các điểm kỳ dị và tính toán thặng dư. Nghiên cứu của Viện Toán học Việt Nam chỉ ra rằng 40% bài toán về số phức đòi hỏi kiến thức vững về phân số.

Việc kết hợp phân số và số phức mở ra nhiều ứng dụng trong kỹ thuật điện tử, xử lý tín hiệu số và thiết kế mạch điện.

Khi khám phá phân số là gì, bạn sẽ nhận thấy đây là khái niệm quan trọng trong toán học, giúp giải quyết nhiều bài toán từ cơ bản đến phức tạp. Bài viết đã cung cấp cái nhìn tổng quan về các thành phần của phân số, cách tính toán, so sánh, cùng ứng dụng thực tế trong đời sống. Kiến thức về phân số không chỉ hữu ích cho học sinh lớp 4 mà còn giúp nền tảng vững chắc cho các môn học nâng cao hơn.