Kiến thức cơ bản về phương trình đường thẳng và cách viết hiệu quả

Phương trình đường thẳng là một phần quan trọng trong toán học, giúp mô tả quan hệ giữa hai biến. Bài viết này sẽ diễn giải các dạng phương trình khác nhau, cung cấp công thức và hướng dẫn chi tiết về cách viết và lập phương trình. Từ đó, bạn có thể áp dụng hiệu quả trong học tập và làm bài tập.

Phương trình đường thẳng và các dạng biểu diễn cơ bản

Trong lý thuyết đại số, phương trình đường thẳng là biểu thức toán học mô tả mối quan hệ giữa tọa độ các điểm nằm trên một đường thẳng trong mặt phẳng tọa độ. Phương trình đường thẳng là công cụ quan trọng để nghiên cứu các tính chất hình học và ứng dụng trong nhiều lĩnh vực thực tiễn.

Phương trình đường thẳng có thể được biểu diễn dưới nhiều dạng khác nhau, mỗi dạng có những ưu điểm riêng và phù hợp với từng bài toán cụ thể. Dạng tổng quát ax + by + c = 0 thường được sử dụng phổ biến nhất do tính đơn giản và dễ áp dụng trong các phép biến đổi.

Một đặc điểm quan trọng của phương trình đường thẳng là tính chất tuyến tính, nghĩa là mọi điểm thuộc đường thẳng đều thỏa mãn một phương trình bậc nhất. Điều này giúp ta dễ dàng xác định vị trí tương đối giữa các đường thẳng cũng như tìm giao điểm của chúng.

Trong thực tế, phương trình đường thẳng được ứng dụng rộng rãi trong kinh tế để mô tả quan hệ cung cầu, trong vật lý để biểu diễn chuyển động thẳng đều, hay trong kỹ thuật xây dựng để thiết kế các công trình. Việc nắm vững các dạng biểu diễn và phương pháp giải sẽ giúp giải quyết hiệu quả nhiều bài toán thực tiễn.

Các dạng phương trình đường thẳng thường gặp trong toán học

Phương trình đường thẳng có dạng khác nhau tùy thuộc vào cách biểu diễn và mục đích sử dụng trong từng bài toán cụ thể. Mỗi dạng phương trình đường thẳng đều có những ưu điểm riêng và phù hợp với những tình huống khác nhau trong hình học phẳng.

Phương trình tổng quát ax + by + c = 0

Phương trình tổng quát ax + by + c = 0 là dạng phổ biến nhất để biểu diễn đường thẳng trong mặt phẳng tọa độ. Trong đó, a và b không đồng thời bằng 0, còn c là hằng số bất kỳ. Dạng này thường được sử dụng khi cần xác định vị trí tương đối giữa hai đường thẳng.

Khi giải các bài toán liên quan đến phương trình vô tỉ lớp 9, việc chuyển về dạng tổng quát sẽ giúp đơn giản hóa quá trình tính toán. Đặc biệt trong trường hợp tìm giao điểm của hai đường thẳng, dạng này cho phép áp dụng phương pháp thế hoặc cộng trừ một cách thuận lợi.

Phương trình tham số của đường thẳng

Phương trình tham số của đường thẳng được biểu diễn dưới dạng:
x = x0 + at
y = y0 + bt
Trong đó (x0, y0) là một điểm thuộc đường thẳng, (a,b) là vector chỉ phương và t là tham số.

Dạng tham số đặc biệt hữu ích khi cần xác định các điểm thuộc đường thẳng thông qua việc thay đổi giá trị của tham số t. Nó cũng thuận tiện trong việc biểu diễn chuyển động của một vật theo thời gian trên đường thẳng.

Phương trình đường thẳng dạng y = mx + n

Phương trình y = mx + n là dạng đơn giản và trực quan nhất, trong đó m là hệ số góc thể hiện độ dốc của đường thẳng, còn n là tung độ gốc – tọa độ điểm mà đường thẳng cắt trục tung. Dạng này giúp dễ dàng nhận biết các đặc điểm hình học của đường thẳng.

Khi m tăng, độ dốc của đường thẳng tăng và ngược lại. Nếu m > 0, đường thẳng đi lên từ trái sang phải. Nếu m < 0, đường thẳng đi xuống từ trái sang phải. Trường hợp m = 0 cho ta đường thẳng song song với trục hoành.

Dạng này thường được ưu tiên sử dụng trong các bài toán về tính đơn điệu và khảo sát hàm số bậc nhất. Nó cũng rất hữu ích khi cần vẽ đồ thị đường thẳng một cách nhanh chóng và chính xác.

Cách viết phương trình đường thẳng qua hai điểm cho trước

Cách viết phương trình đường thẳng là một kỹ năng quan trọng trong hình học giải tích. Khi có hai điểm cho trước, ta có thể xác định duy nhất một đường thẳng đi qua chúng và biểu diễn nó bằng phương trình toán học.

Để xác định phương trình đường thẳng qua hai điểm, ta cần thực hiện các bước có tính hệ thống. Quá trình này bao gồm việc xác định vector chỉ phương, tính toán các hệ số và lập phương trình cuối cùng. Tương tự như phương trình đường tròn, phương trình đường thẳng cũng tuân theo các quy tắc toán học chặt chẽ.

Các bước xác định vector chỉ phương

Vector chỉ phương là yếu tố then chốt để xác định hướng của đường thẳng trong không gian. Khi có hai điểm A(x₁,y₁) và B(x₂,y₂), vector chỉ phương được tính bằng hiệu vector của hai điểm này.

Vector chỉ phương v⃗ = (x₂-x₁, y₂-y₁) sẽ cho ta thông tin về độ dốc của đường thẳng. Độ lớn của vector không ảnh hưởng đến phương trình đường thẳng, chỉ hướng của nó mới quan trọng.

Phương pháp tính toán và lập phương trình

Sau khi có vector chỉ phương, ta sử dụng phương pháp tham số để viết phương trình đường thẳng. Phương trình tham số có dạng: x = x₁ + t(x₂-x₁), y = y₁ + t(y₂-y₁), với t là tham số.

Từ phương trình tham số, ta có thể chuyển về dạng tổng quát Ax + By + C = 0 bằng cách loại tham số t. Phương trình này là dạng chuẩn và thường được sử dụng nhiều nhất trong các bài toán hình học.

Ngoài ra, ta cũng có thể biểu diễn dưới dạng y = mx + b, với m là hệ số góc và b là tung độ gốc. Hệ số góc m được tính bằng (y₂-y₁)/(x₂-x₁).

Ví dụ minh họa chi tiết

Cho hai điểm A(1,2) và B(4,5), ta sẽ lập phương trình đường thẳng đi qua hai điểm này.

Bước 1: Tính vector chỉ phương
v⃗ = (4-1, 5-2) = (3,3)

Bước 2: Lập phương trình tham số
x = 1 + 3t
y = 2 + 3t

Bước 3: Chuyển về dạng tổng quát
Loại t từ hai phương trình trên:
(x-1)/3 = (y-2)/3
3(y-2) = 3(x-1)
y – 2 = x – 1
y = x + 1

Vậy phương trình đường thẳng qua hai điểm A và B là y = x + 1.

Phương pháp lập phương trình đường thẳng trong hình học phẳng

Cách lập phương trình đường thẳng trong hình học phẳng dựa trên các yếu tố đặc trưng như vector chỉ phương, điểm đi qua và góc nghiêng với trục hoành. Phương pháp này giúp biểu diễn chính xác vị trí và hướng của đường thẳng trên mặt phẳng tọa độ.

Việc lập phương trình đường thẳng cần xác định rõ các thông số cơ bản như hệ số góc và tung độ gốc. Các thông số này có thể được tính toán thông qua các điều kiện cho trước như hai điểm đi qua, góc nghiêng với trục hoành hoặc quan hệ song song/vuông góc với đường thẳng khác.

Để áp dụng hiệu quả, ta có thể sử dụng phương trình tiếp tuyến làm công cụ hỗ trợ khi cần xác định đường thẳng tiếp xúc với đường cong. Điều này đặc biệt hữu ích trong các bài toán hình học phức tạp.

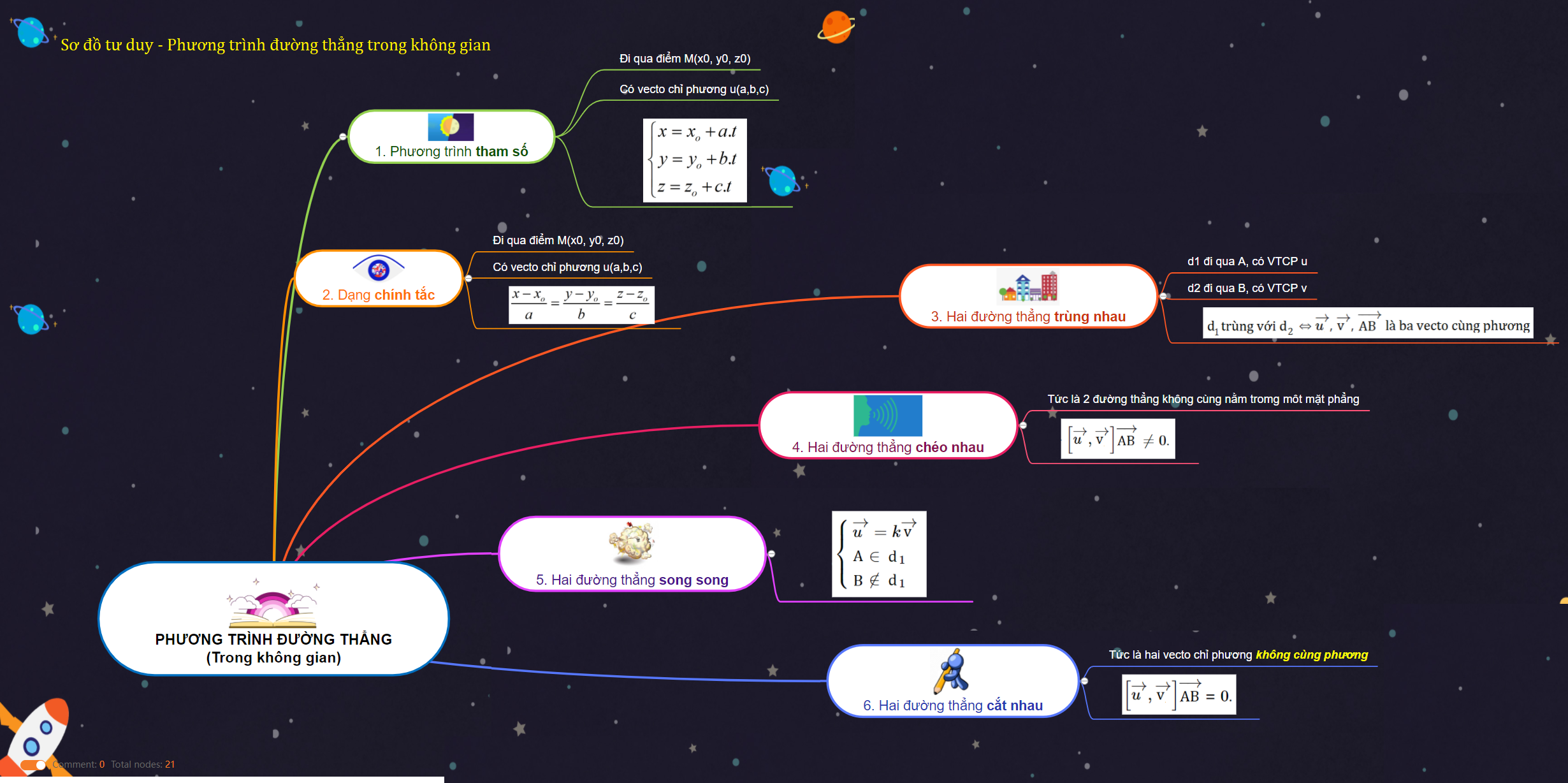
Phương trình đường thẳng song song

Khi hai đường thẳng song song, chúng có cùng hệ số góc nhưng khác tung độ gốc. Đây là đặc trưng quan trọng để xác định phương trình đường thẳng song song với một đường thẳng cho trước.

Nếu đường thẳng d1 có phương trình y = ax + b, thì đường thẳng d2 song song với d1 sẽ có dạng y = ax + k, trong đó k là một hằng số khác b. Giá trị của k được xác định dựa vào điều kiện bổ sung như điểm đi qua hoặc khoảng cách giữa hai đường thẳng.

Ví dụ thực tế từ kiến trúc: Khi thiết kế đường ray tàu điện, các kỹ sư phải đảm bảo hai đường ray luôn song song và cách đều nhau. Theo tiêu chuẩn của Tổng công ty Đường sắt Việt Nam, khoảng cách giữa hai đường ray phải duy trì ở mức 1,435m để đảm bảo an toàn.

Phương trình đường thẳng vuông góc

Hai đường thẳng vuông góc có tích các hệ số góc bằng -1. Nguyên tắc này là cơ sở để xác định phương trình đường thẳng vuông góc với đường thẳng cho trước.

Khi một đường thẳng có hệ số góc a, đường thẳng vuông góc với nó sẽ có hệ số góc -1/a. Điều này áp dụng cho mọi trường hợp, trừ khi đường thẳng ban đầu song song với trục tung.

Trong thực tế, nguyên lý này được ứng dụng rộng rãi trong xây dựng. Các bức tường vuông góc trong nhà phải đảm bảo góc 90 độ để tạo không gian sống tiện nghi và thẩm mỹ.

Phương trình đường thẳng đi qua một điểm

Phương trình đường thẳng đi qua điểm M(x0, y0) có thể được viết dưới dạng y – y0 = a(x – x0), trong đó a là hệ số góc của đường thẳng. Công thức này áp dụng cho mọi điểm thuộc đường thẳng.

Trong trường hợp biết thêm một điểm thứ hai N(x1, y1), hệ số góc được tính bằng tỷ số (y1 – y0)/(x1

Ứng dụng phương trình đường thẳng trong chương trình toán lớp 10

Phương trình đường thẳng lớp 10 có nhiều ứng dụng quan trọng trong việc giải các bài toán hình học. Việc nắm vững kiến thức về phương trình đường thẳng giúp học sinh dễ dàng giải quyết các dạng toán về khoảng cách, góc và giao điểm.

Khi áp dụng phương trình đường thẳng vào giải toán, học sinh cần kết hợp với các kiến thức về phương trình chính tắc của parabol và phương trình elip có dạng để giải quyết các bài toán phức tạp hơn.

Bài toán về khoảng cách

Bài toán về khoảng cách thường yêu cầu tìm khoảng cách từ một điểm đến đường thẳng hoặc khoảng cách giữa hai đường thẳng song song. Để giải quyết dạng bài này, cần sử dụng công thức tính khoảng cách từ điểm đến đường thẳng.

Việc áp dụng công thức khoảng cách cần chú ý đến dấu của các hệ số trong phương trình đường thẳng. Khi tính khoảng cách giữa hai đường thẳng song song, cần đưa phương trình về dạng chuẩn tắc trước.

Bài toán về góc

Góc giữa hai đường thẳng được xác định thông qua vector pháp tuyến hoặc vector chỉ phương của chúng. Khi giải bài toán về góc, việc quan trọng là xác định được hệ số góc của các đường thẳng.

Trong nhiều trường hợp, bài toán yêu cầu tìm góc giữa đường thẳng với trục tọa độ hoặc với một đường thẳng cho trước. Việc sử dụng công thức tính góc giữa hai đường thẳng sẽ giúp giải quyết nhanh chóng các bài toán này.

Bài toán về giao điểm

Tìm giao điểm của hai đường thẳng là một trong những ứng dụng cơ bản của hệ phương trình bậc nhất hai ẩn. Khi hai đường thẳng không song song, chúng sẽ cắt nhau tại một điểm duy nhất.

Phương pháp giải bài toán giao điểm thường bắt đầu bằng việc lập hệ phương trình từ hai đường thẳng đã cho. Sau đó sử dụng các phương pháp giải hệ phương trình như phương pháp thế, phương pháp cộng đại số để tìm tọa độ giao điểm.

Việc xét các trường hợp đặc biệt như đường thẳng song song hoặc trùng nhau cũng rất quan trọng trong quá trình giải bài toán giao điểm. Điều này giúp đưa ra kết luận chính xác về số lượng giao điểm của hai đường thẳng.

Các công thức và phương pháp tính nhanh trong phương trình đường thẳng

Việc nắm vững các công thức phương trình đường thẳng giúp giải quyết nhanh chóng nhiều bài toán hình học phẳng. Tương tự như công thức fibonacci, các công thức này tạo nền tảng quan trọng cho việc học toán nâng cao.

Để tìm phương trình đường thẳng một cách hiệu quả, việc áp dụng đúng công thức phù hợp với từng dạng bài toán là rất quan trọng. Các phương pháp tính nhanh thường được áp dụng khi có đủ các yếu tố như vector chỉ phương, điểm đi qua hay hệ số góc của đường thẳng.

Công thức tính khoảng cách từ điểm đến đường thẳng

Khoảng cách từ điểm M(x0,y0) đến đường thẳng ax + by + c = 0 được tính bằng công thức: d = |ax0 + by0 + c|/√(a² + b²). Công thức này có ý nghĩa quan trọng trong việc xác định vị trí tương đối giữa điểm và đường thẳng.

Việc áp dụng công thức trên có thể kết hợp với phương trình mặt phẳng trung trực để giải các bài toán phức tạp hơn trong không gian. Điều này được chứng minh qua nhiều ứng dụng thực tế trong kiến trúc và xây dựng.

Theo các chuyên gia từ Hocthenao.vn, việc thành thạo công thức này giúp học sinh tiết kiệm thời gian giải toán và nâng cao điểm số trong các kỳ thi quan trọng.

Công thức tính góc giữa hai đường thẳng

Góc giữa hai đường thẳng d1: y = k1x + b1 và d2: y = k2x + b2 được tính theo công thức: tanα = |k1 – k2|/(1 + k1k2). Công thức này áp dụng cho trường hợp góc nhọ giữa hai đường thẳng.

Khi hai đường thẳng cho dưới dạng tổng quát a1x + b1y + c1 = 0 và a2x + b2y + c2 = 0, góc giữa chúng được tính bằng: cosα = |a1a2 + b1b2|/√((a1² + b1²)(a2² + b2²)). Đây là công thức tổng quát áp dụng cho mọi trường hợp.

Trong thực tế, việc tính góc giữa hai đường thẳng có ý nghĩa quan trọng trong nhiều lĩnh vực như thiết kế đồ họa, xây dựng và kiến trúc. Ví dụ, khi thiết kế mái nhà, kiến trúc sư cần tính toán chính xác góc nghiêng để đảm bảo độ bền và thoát nước hiệu quả.

Để nắm vững phương trình đường thẳng, bạn cần hiểu rõ các dạng biểu diễn cơ bản cũng như cách lập và viết phương trình một cách chính xác. Việc áp dụng các công thức và phương pháp tính toán nhanh sẽ giúp bạn tự tin hơn trong giải quyết các bài toán liên quan. Hãy bắt đầu áp dụng ngay hôm nay để trở thành người thành thạo trong môn toán!