Phương trình elip: Định nghĩa, tính chất và ứng dụng trong toán học lớp 10

Phương trình elip là một trong những khái niệm quan trọng trong hình học, giúp mô tả đường cong bầu dục. Bài viết này sẽ cung cấp các dạng phương trình, tính chất và ứng dụng của elip, cùng với hướng dẫn vẽ đồ thị và tính toán diện tích. Khám phá ngay để nắm vững kiến thức này!

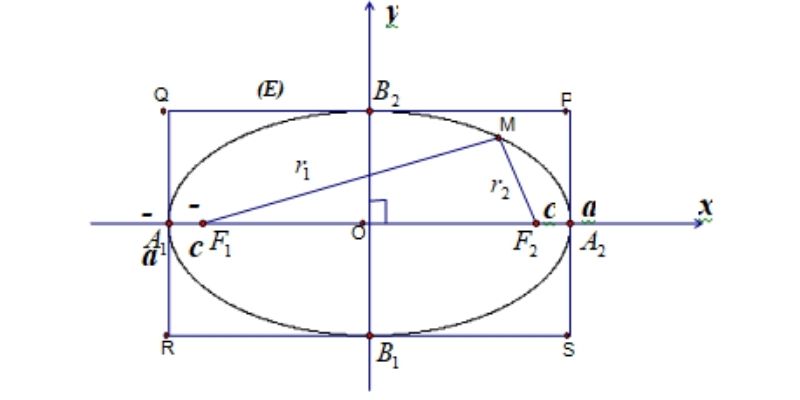
Phương trình elip là phương trình toán học biểu diễn đường cong kín dạng bầu dục

Phương trình elip là một dạng phương trình bậc hai biểu diễn đường cong kín có dạng bầu dục, được tạo thành từ tập hợp các điểm có tổng khoảng cách đến hai điểm cố định (tiêu điểm) là không đổi. Đây là một trong những đường cong conic quan trọng trong hình học giải tích.

Phương trình đường elip trong hệ tọa độ Descartes có dạng chuẩn là (x²/a²) + (y²/b²) = 1, trong đó a và b lần lượt là độ dài nửa trục lớn và nửa trục nhỏ của elip. Các thông số này quyết định hình dạng và kích thước của đường elip, với a luôn lớn hơn hoặc bằng b.

Elip có nhiều ứng dụng thực tiễn quan trọng trong khoa học và kỹ thuật. Chẳng hạn như trong thiên văn học, quỹ đạo của các hành tinh quanh Mặt Trời có dạng elip với Mặt Trời nằm tại một tiêu điểm. Trong kiến trúc, hình dạng elip thường được sử dụng để thiết kế mái vòm và các công trình có tính thẩm mỹ cao.

Các dạng phương trình chuẩn tắc của đường elip trong hệ tọa độ Oxy

Phương trình đường chuẩn của elip có nhiều dạng khác nhau tùy thuộc vào vị trí và hướng của trục chính. Phương trình chính tắc của elip là dạng phương trình đơn giản nhất mô tả đường elip, thường được sử dụng làm cơ sở để nghiên cứu các tính chất hình học.

Khi xét phương trình elip có dạng tổng quát, ta cần xác định vị trí tâm và hướng của trục chính để chuyển về dạng chuẩn tắc phù hợp. Việc chuyển đổi này giúp đơn giản hóa các phép tính và phân tích hình học.

Phương trình elip có trục chính song song với trục hoành

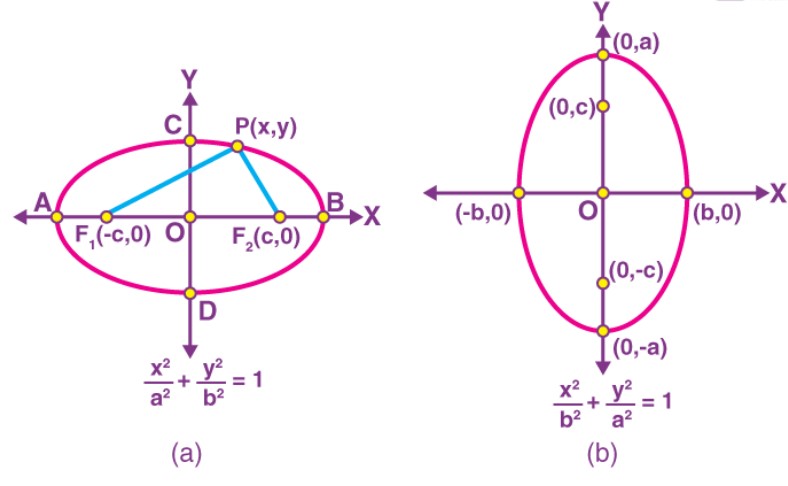
Khi trục chính của elip song song với trục Ox, phương trình có dạng chuẩn tắc là (x-h)²/a² + (y-k)²/b² = 1, trong đó (h,k) là tọa độ tâm elip, a là nửa trục lớn và b là nửa trục bé.

Đối với trường hợp đặc biệt khi tâm elip trùng với gốc tọa độ O(0,0), phương trình được đơn giản hóa thành x²/a² + y²/b² = 1. Điều này tạo thuận lợi cho việc khảo sát các tính chất hình học của elip.

Các tham số a và b trong phương trình quyết định độ dẹt của elip, với a > b tạo nên elip nằm ngang và ngược lại.

Phương trình elip có trục chính song song với trục tung

Khi trục chính của elip song song với trục Oy, phương trình chuẩn tắc có dạng (x-h)²/b² + (y-k)²/a² = 1. Trong trường hợp này, nửa trục lớn a nằm dọc theo trục tung.

Tương tự như trường hợp trước, khi tâm elip trùng với gốc tọa độ, phương trình trở thành x²/b² + y²/a² = 1. Sự thay đổi vị trí của các hệ số a và b so với dạng nằm ngang phản ánh sự xoay 90° của elip.

Việc xác định chính xác dạng phương trình này rất quan trọng trong các ứng dụng thực tế như thiết kế quỹ đạo vệ tinh hay tính toán quang học.

Phương trình elip tổng quát và cách chuyển về dạng chính tắc

Phương trình tổng quát của elip có dạng Ax² + By² + Cx + Dy + E = 0, với A và B cùng dấu. Để chuyển đổi phương trình elip về dạng chuẩn tắc, ta thực hiện phương pháp hoàn chỉnh bình phương.

Quá trình chuyển đổi bao gồm việc tách các số hạng chứa x và y, sau đó hoàn chỉnh bình phương từng nhóm. Phương pháp này giúp xác định được tọa độ tâm và các tham số của elip.

Việc nắm vững cách chuyển đổi này có ý nghĩa quan trọng trong việc giải các bài toán hình học phức tạp, đặc biệt là các bài toán liên quan đến quỹ đạo chuyển động của các vật thể trong vật lý.

Các tính chất quan trọng của đường elip trong toán học lớp 10

Đường elip là một trong những đường conic cơ bản và có nhiều ứng dụng quan trọng trong toán học và thực tế. Tính chất elip được nghiên cứu kỹ lưỡng trong chương trình toán học lớp 10, giúp học sinh nắm vững kiến thức nền tảng về hình học giải tích.

Để hiểu rõ về đường elip, cần nắm được các đặc điểm cơ bản như định nghĩa, tính chất đối xứng và các yếu tố đặc trưng. Những kiến thức này có mối liên hệ chặt chẽ với phương trình đường tròn và các đường conic khác.

Định nghĩa và đặc điểm hình học của elip

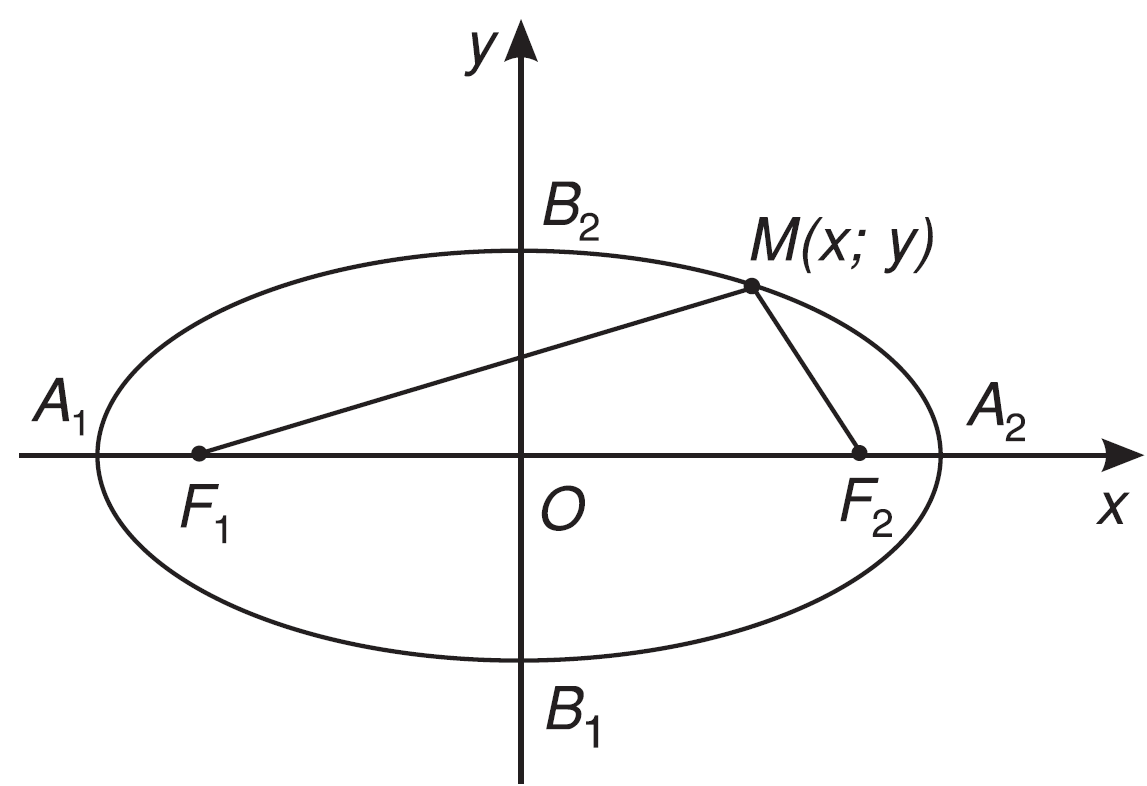
Định nghĩa elip là tập hợp các điểm trong mặt phẳng sao cho tổng khoảng cách từ một điểm bất kỳ đến hai điểm cố định (gọi là tiêu điểm) là một hằng số. Đây là một trong những khái niệm cơ bản nhất khi học về elip lớp 10.

Về mặt hình học, elip có dạng một đường cong kín, trơn và không có điểm gấp khúc. Hình dạng của elip phụ thuộc vào khoảng cách giữa hai tiêu điểm và độ dài trục chính. Khi hai tiêu điểm trùng nhau, elip trở thành đường tròn.

Tâm đối xứng và trục đối xứng của elip

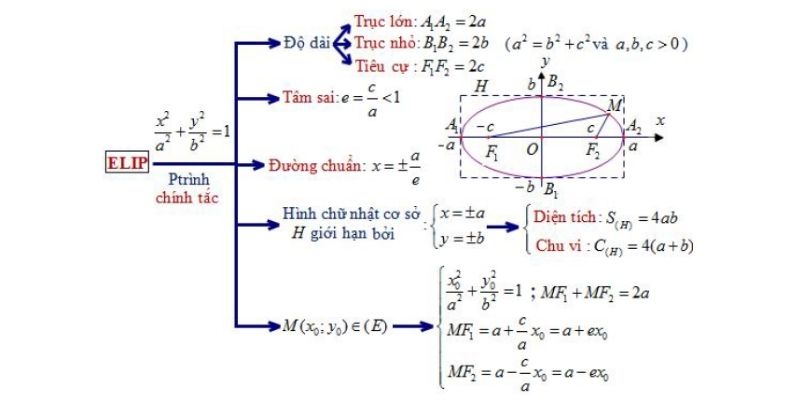
Elip có hai trục đối xứng vuông góc với nhau đi qua tâm. Trục chính là trục đối xứng chứa hai tiêu điểm, còn trục phụ vuông góc với trục chính tại tâm elip. Điểm giao của hai trục này chính là tâm đối xứng của elip.

Tính chất đối xứng của elip thể hiện qua việc mọi điểm trên elip đều có điểm đối xứng qua tâm và qua hai trục. Đặc điểm này giúp đơn giản hóa việc vẽ và tính toán các yếu tố liên quan đến elip trục chính.

Tiêu điểm và độ lệch tâm của elip

Hai tiêu điểm là yếu tố quan trọng quyết định hình dạng của elip. Khoảng cách từ tâm đến tiêu điểm được gọi là tiêu cự. Tỷ số giữa tiêu cự và độ dài nửa trục chính được gọi là độ lệch tâm, là một đại lượng đặc trưng cho độ “dẹt” của elip.

Độ lệch tâm luôn nhỏ hơn 1 và càng gần 1 thì elip càng dẹt. Ngược lại, khi độ lệch tâm tiến về 0, elip sẽ tiến đến hình dạng của đường tròn. Đây là một trong những tính chất quan trọng giúp phân biệt elip với các đường conic khác.

Phương pháp vẽ đồ thị và tính toán các yếu tố của elip

Việc vẽ và tính toán các yếu tố của đồ thị elip đòi hỏi sự hiểu biết về các thành phần cơ bản như tâm, tiêu điểm và trục. Các phương pháp này giúp giải quyết nhiều bài toán hình học phức tạp liên quan đến phương trình elip. Để thực hiện chính xác, cần nắm vững các công thức và quy tắc vẽ cơ bản.

Các bước vẽ đồ thị elip từ phương trình

Bước đầu tiên là xác định tâm elip thông qua việc đưa phương trình về dạng chuẩn tắc. Quá trình này có thể yêu cầu sử dụng phương pháp gauss để biến đổi ma trận hệ số.

Tiếp theo, xác định độ dài trục lớn và trục nhỏ bằng cách tính các hệ số trong phương trình. Các giá trị này sẽ quyết định hình dạng của elip.

Cuối cùng, vẽ các điểm đặc biệt như đỉnh và tiêu điểm, sau đó nối các điểm theo quy luật để tạo thành đường cong elip hoàn chỉnh.

Cách xác định diện tích elip và chu vi gần đúng

Diện tích elip được tính chính xác thông qua công thức π.a.b, trong đó a và b lần lượt là độ dài nửa trục lớn và nửa trục nhỏ. Phương pháp này áp dụng cho mọi elip, không phụ thuộc vào vị trí hay hướng của các trục.

Đối với chu vi, do không có công thức chính xác, người ta thường sử dụng công thức gần đúng của Ramanujan. Công thức này cho kết quả với độ chính xác cao, đủ để áp dụng trong hầu hết các bài toán thực tế.

Trong nhiều trường hợp, việc tính toán có thể đơn giản hóa bằng cách sử dụng các phần mềm đồ họa chuyên dụng hoặc máy tính khoa học.

Phương pháp tìm giao điểm của elip với đường thẳng

Để tìm giao điểm, cần thay phương trình đường thẳng vào phương trình elip. Quá trình này thường dẫn đến một phương trình vô tỉ cần được giải quyết.

Phương pháp giải phương trình thu được có thể thực hiện thông qua việc đặt ẩn phụ hoặc biến đổi về dạng phương trình bậc hai. Số nghiệm của phương trình sẽ cho biết số giao điểm giữa elip và đường thẳng.

Trong trường hợp đặc biệt, khi đường thẳng tiếp xúc với elip, phương trình sẽ có nghiệm kép, và khi đường thẳng cắt elip, phương trình sẽ có hai nghiệm phân biệt.

Ứng dụng của phương trình elip trong thực tế và khoa học

Phương trình elip có nhiều ứng dụng quan trọng trong đời sống và khoa học. Từ việc mô tả quỹ đạo chuyển động của các hành tinh cho đến thiết kế công trình kiến trúc, lý thuyết elip đã chứng minh được vai trò không thể thiếu trong nhiều lĩnh vực.

Không chỉ dừng lại ở mặt lý thuyết thuần túy như đường parabol, các ứng dụng elip còn góp phần giải quyết nhiều bài toán thực tiễn trong công nghiệp và đời sống. Việc hiểu và vận dụng đúng tính chất của elip giúp con người tối ưu hóa nhiều thiết kế và quy trình sản xuất.

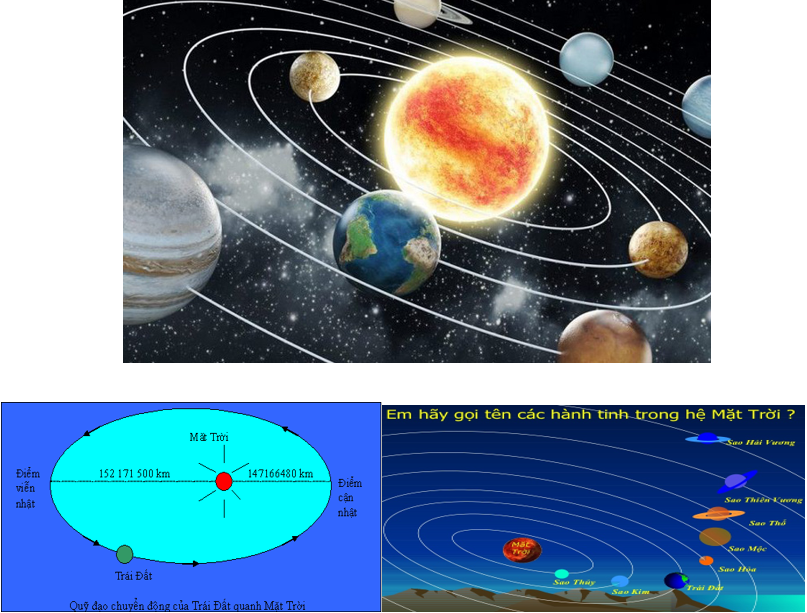
Ứng dụng trong thiên văn học và quỹ đạo hành tinh

Johannes Kepler đã chứng minh rằng các hành tinh chuyển động quanh Mặt Trời theo quỹ đạo elip, với Mặt Trời nằm tại một tiêu điểm. Phát hiện này đã mở ra một kỷ nguyên mới trong nghiên cứu thiên văn học.

Các vệ tinh nhân tạo cũng được thiết kế để di chuyển theo quỹ đạo elip quanh Trái Đất. NASA đã áp dụng tính toán quỹ đạo elip để đưa tàu vũ trụ Apollo lên Mặt Trăng thành công vào năm 1969.

Ứng dụng trong kiến trúc và nghệ thuật

Hình dạng elip được ứng dụng rộng rãi trong thiết kế kiến trúc nhờ tính thẩm mỹ và khả năng chịu lực tốt. Nhà thờ St. Peter’s Square tại Vatican là một ví dụ điển hình với quảng trường hình elip rộng lớn.

Trong nghệ thuật, elip thường xuất hiện trong các tác phẩm hội họa và điêu khắc để tạo cảm giác hài hòa, cân đối. Nhiều họa sĩ thời kỳ Phục Hưng đã sử dụng elip như một công cụ để tạo chiều sâu và phối cảnh trong tranh.

Ứng dụng trong âm học và quang học

Trong phòng thì thầm, âm thanh phát ra từ một tiêu điểm của elip sẽ được phản xạ và hội tụ tại tiêu điểm còn lại. Nguyên lý này được ứng dụng trong thiết kế phòng hòa nhạc và nhà hát để tối ưu hóa âm thanh.

Tính chất phản xạ của elip còn được ứng dụng trong chế tạo gương phản xạ cho kính thiên văn và các thiết bị quang học. Các tấm gương hình elip giúp tập trung ánh sáng hiệu quả hơn so với gương cầu thông thường.

Trong y học, máy tán sỏi thận sử dụng nguyên lý phản xạ sóng âm qua mặt elip để phá vỡ sỏi mà không cần phẫu thuật xâm lấn. Đây là một trong những ứng dụng quan trọng của elip trong điều trị bệnh.

Phương trình elip là một khái niệm quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về hình học và ứng dụng thực tiễn của nó. Nội dung bài viết đã cung cấp các dạng phương trình khác nhau, những tính chất nổi bật và các bước vẽ đồ thị elip. Đừng bỏ lỡ cơ hội nắm vững kiến thức với những ứng dụng thú vị trong khoa học và thực tiễn mà elip mang lại.