Tích có hướng của 2 vecto: Công thức, cách tính và ứng dụng trong toán học

Tích có hướng của 2 vecto là một phép toán quan trọng trong hình học không gian, tạo ra vecto mới vuông góc với hai vecto ban đầu. Bài viết giới thiệu công thức, cách tính và ứng dụng của tích có hướng, giúp bạn hiểu rõ hơn về đặc điểm và tính chất của nó trong toán học và vật lý.

Tích có hướng của 2 vecto là phép toán tạo ra vecto mới vuông góc với cả hai vecto ban đầu

Tích có hướng của 2 vecto là phép toán tạo ra một vecto mới có phương vuông góc với mặt phẳng chứa hai vecto ban đầu. Vecto kết quả này chính là vector pháp tuyến của mặt phẳng đó.

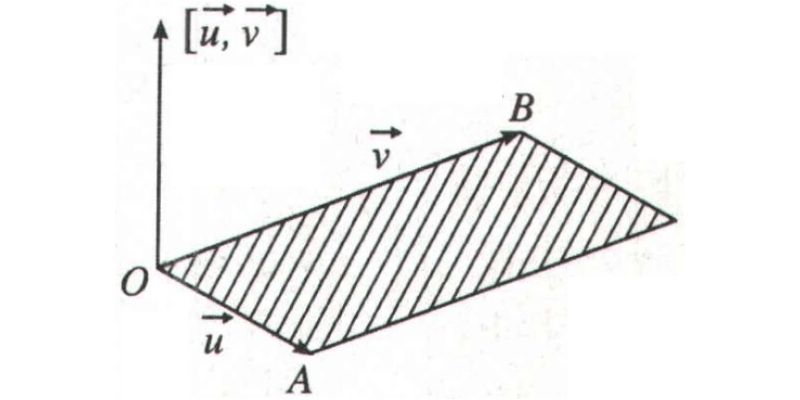
Khi thực hiện phép tích có hướng là gì, ta sẽ nhận được một vecto mới có độ lớn bằng tích độ lớn của hai vecto nhân với sin của góc giữa chúng. Chiều của vecto kết quả được xác định theo quy tắc bàn tay phải – khi ngón cái chỉ theo chiều vecto kết quả thì các ngón còn lại quét từ vecto thứ nhất đến vecto thứ hai theo góc nhỏ nhất.

Phép toán này có ý nghĩa quan trọng trong nhiều lĩnh vực như vật lý, kỹ thuật và toán học ứng dụng. Ví dụ trong cơ học, tích có hướng được sử dụng để tính moment của lực, trong điện từ học nó giúp xác định hướng của từ trường sinh ra bởi dòng điện chạy trong dây dẫn.

Công thức tính tích có hướng và các thành phần cơ bản

Công thức tính tích có hướng của hai vectơ a và b được xác định bằng biểu thức: [a,b] = |a|.|b|.sin(α), trong đó α là góc giữa hai vectơ. Kết quả của phép tính này là một vectơ vuông góc với cả hai vectơ ban đầu và có độ lớn bằng diện tích hình bình hành tạo bởi chúng.

Tích có hướng còn được gọi là tích vector, là một phép toán quan trọng trong hình học vector và vật lý. Khác với tích vô hướng của hai vectơ, kết quả của phép tính này là một vectơ mới có hướng xác định theo quy tắc bàn tay phải.

Biểu diễn tích có hướng qua định thức

Tích có hướng của hai vectơ có thể biểu diễn dưới dạng định thức cấp 3, với i, j, k là các vector đơn vị của hệ trục tọa độ:
|i j k|
|a1 a2 a3|
|b1 b2 b3|

Cách biểu diễn này giúp việc tính toán trở nên có hệ thống và chính xác hơn. Khi triển khai định thức, ta sẽ thu được các thành phần của vector kết quả theo từng phương.

Tính tích có hướng bằng tọa độ trong không gian Oxyz

Cách tính tích có hướng trong hệ tọa độ Oxyz được thực hiện thông qua công thức:
[a,b] = (a2b3 – a3b2)i + (a3b1 – a1b3)j + (a1b2 – a2b1)k

Phương pháp này đặc biệt hữu ích khi làm việc với các bài toán trong không gian ba chiều. Mỗi thành phần của vector kết quả được tính độc lập, giúp kiểm soát được độ chính xác của phép tính.

Mối liên hệ giữa độ dài tích có hướng và diện tích hình bình hành

Độ dài của tích có hướng của 2 vectơ oxyz có mối liên hệ trực tiếp với diện tích hình bình hành được tạo bởi hai vectơ đó. Cụ thể, độ dài của tích có hướng chính bằng diện tích hình bình hành.

Mối liên hệ này có ý nghĩa quan trọng trong nhiều ứng dụng thực tế, từ tính toán moment lực trong cơ học đến xác định diện tích trong hình học không gian. Đây là một trong những lý do khiến tích có hướng trở thành công cụ không thể thiếu trong toán học và vật lý.

Đặc điểm và tính chất quan trọng của tích có hướng

Đặc điểm tích có hướng là một phép toán quan trọng trong hình học vector, cho phép tính toán góc giữa hai vector và độ lớn của chúng. Kết quả của phép nhân này là một số vô hướng, thể hiện mối quan hệ hình học giữa hai vector trong không gian.

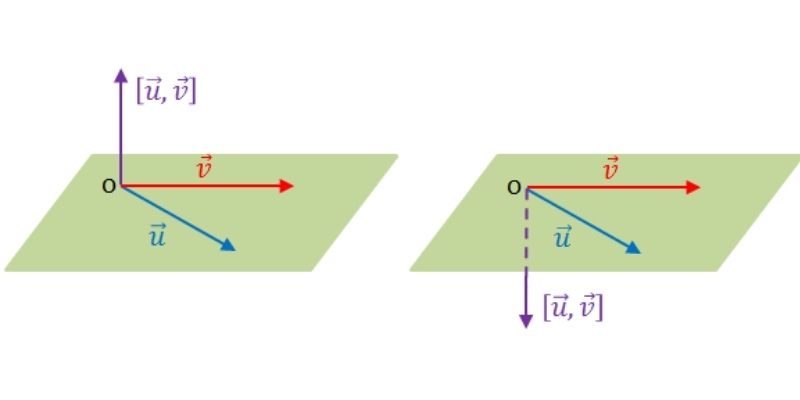
Tích có hướng của 2 vecto được xác định bởi độ lớn của hai vector và góc giữa chúng, tạo nên một công cụ đắc lực để giải quyết nhiều bài toán hình học phức tạp. Phép toán này có những tính chất đặc biệt giúp đơn giản hóa các phép tính và chứng minh trong không gian vector.

Tính phản giao hoán của tích có hướng

Tích có hướng không tuân theo quy tắc giao hoán thông thường. Khi đổi vị trí hai vector trong phép nhân, kết quả sẽ đổi dấu. Điều này được biểu diễn qua công thức: a×b = -(b×a).

Tính chất này có ý nghĩa quan trọng trong việc xác định chiều của vector pháp tuyến và giải quyết các bài toán liên quan đến moment lực trong vật lý. Nó cũng giúp phân biệt rõ thứ tự của các vector trong các phép tính phức tạp.

Tính chất phân phối đối với phép cộng

Tích có hướng tuân theo quy luật phân phối đối với phép cộng vector. Điều này được thể hiện qua công thức: a×(b+c) = a×b + a×c.

Tính chất này cho phép chia nhỏ các phép tính phức tạp thành những phép tính đơn giản hơn. Nó đặc biệt hữu ích khi giải quyết các bài toán liên quan đến tổng của nhiều vector hoặc khi cần phân tích một vector thành tổng của các thành phần.

Điều kiện để tích có hướng bằng 0

Tích có hướng của hai vector bằng 0 khi và chỉ khi điều kiện 2 vecto cùng phương hoặc ít nhất một trong hai vector có độ dài bằng 0.

Điều kiện này có ý nghĩa hình học sâu sắc, phản ánh mối quan hệ song song hoặc trùng phương giữa các vector. Nó thường được áp dụng trong việc kiểm tra tính song song của các đường thẳng và mặt phẳng trong không gian ba chiều.

Việc hiểu rõ điều kiện này giúp giải quyết nhiều bài toán về vector một cách hiệu quả, đặc biệt trong các ứng dụng về động lực học và hình học không gian.

Ứng dụng tích có hướng trong hình học không gian và vật lý

Ứng dụng tích có hướng là một công cụ toán học quan trọng giúp giải quyết nhiều bài toán trong lý thuyết hình học không gian và vật lý. Phép tính này cho phép xác định phương, chiều và độ lớn của các đại lượng vectơ trong không gian ba chiều.

Tích có hướng được ứng dụng rộng rãi trong nhiều lĩnh vực, từ tính toán diện tích, thể tích đến xác định moment lực trong cơ học. Việc nắm vững cách áp dụng tích có hướng sẽ giúp giải quyết hiệu quả các bài toán vectơ trong không gian.

Tìm vecto pháp tuyến của mặt phẳng

Tích có hướng giúp xác định vectơ pháp tuyến của mặt phẳng thông qua hai vectơ chỉ phương nằm trên mặt phẳng đó. Khi có hai vectơ a và b nằm trên mặt phẳng, vectơ pháp tuyến n được tính bằng tích có hướng của hai vectơ này: n = a × b.

Phương pháp này đặc biệt hữu ích trong các bài toán xác định phương trình mặt phẳng. Vectơ pháp tuyến cho biết hướng vuông góc với mặt phẳng, từ đó có thể viết phương trình tổng quát của mặt phẳng dưới dạng: Ax + By + Cz + D = 0.

Tính diện tích hình bình hành và tam giác

Diện tích hình bình hành được xác định bằng độ lớn của tích có hướng giữa hai vectơ cạnh. Với hai vectơ a và b là hai cạnh kề của hình bình hành, diện tích S = |a × b|. Phương pháp này cho kết quả chính xác và nhanh chóng hơn so với các cách tính truyền thống.

Đối với tam giác, diện tích được tính bằng một nửa diện tích hình bình hành tương ứng. Nếu A, B, C là ba đỉnh của tam giác, ta có thể tính diện tích thông qua hai vectơ AB và AC: S = (1/2)|AB × AC|.

Ứng dụng trong tính moment lực và moment động lượng

Moment lực đóng vai trò quan trọng trong việc nghiên cứu chuyển động quay của vật thể. Moment lực M được tính bằng tích có hướng của vectơ khoảng cách r (từ trục quay đến điểm đặt lực) với vectơ lực F: M = r × F.

Tương tự, moment động lượng L của một vật được tính bằng tích có hướng của vectơ vị trí r với vectơ động lượng p: L = r × p. Các công thức này giúp phân tích và dự đoán chuyển động của vật trong các bài toán cơ học phức tạp.

Phương pháp giải bài tập về tích có hướng hiệu quả

Việc nắm vững tích có hướng của hai vectơ là nền tảng quan trọng để giải quyết nhiều bài toán trong hình học không gian. Phương pháp giải hiệu quả đòi hỏi sự kết hợp giữa kiến thức lý thuyết và kỹ năng tính toán.

Để giải thành công các bài tập về tích có hướng, cần nắm chắc công thức tính và ý nghĩa hình học của nó. Đặc biệt quan trọng là hiểu rõ mối liên hệ với tính góc giữa 2 vecto để áp dụng vào các bài toán thực tế.

Các dạng bài tập thường gặp

Trong chương trình vectơ và phương trình, có một số dạng bài tập điển hình về tích có hướng. Dạng thứ nhất là tính tích có hướng khi biết tọa độ hai vectơ. Dạng thứ hai là tìm góc giữa hai vectơ thông qua tích có hướng.

Dạng thứ ba là ứng dụng tích có hướng để tính diện tích tam giác, tứ giác. Dạng thứ tư là sử dụng tích có hướng để kiểm tra tính vuông góc của hai vectơ.

Quy trình giải và kiểm tra kết quả

Bước đầu tiên là phân tích kỹ đề bài, xác định rõ dữ kiện và yêu cầu. Tiếp theo là lựa chọn phương pháp giải phù hợp dựa trên tính chất của tích có hướng.

Trong quá trình giải, cần kiểm tra tính hợp lý của kết quả trung gian. Cuối cùng là đối chiếu đáp số với điều kiện bài toán và thực hiện phép kiểm tra ngược.

Việc áp dụng Website về môn toán sẽ giúp củng cố kiến thức và rèn luyện kỹ năng giải bài tập hiệu quả.

Một số bài tập minh họa có lời giải

Bài tập 1: Cho hai vectơ a(2,3) và b(-1,4). Tính tích có hướng của hai vectơ này.
Lời giải: Áp dụng công thức tích có hướng: a.b = 2.(-1) + 3.4 = -2 + 12 = 10

Bài tập 2: Cho tam giác ABC có A(0,0), B(2,0), C(1,2). Tính diện tích tam giác ABC.
Lời giải: Diện tích tam giác bằng một nửa độ lớn tích có hướng của hai vectơ AB và AC.
S = 1/2.|AB x AC| = 1/2.|2.2| = 2 (đơn vị diện tích)

Tích có hướng của 2 vecto là một phép toán quan trọng trong hình học không gian, giúp xác định vecto mới vuông góc với cả hai vecto ban đầu. Qua các công thức và đặc điểm được trình bày, người học có thể dễ dàng áp dụng và thực hành cách tính tích có hướng trong các bài toán thực tiễn, từ việc tính toán diện tích hình bình hành đến việc xác định vecto pháp tuyến. Hãy khám phá và áp dụng kiến thức này để nâng cao khả năng về vecto trong toán học!