Khái niệm và ứng dụng của vecto pháp tuyến trong hình học toán học

Vecto pháp tuyến là gì? Đây là một khái niệm quan trọng trong hình học giúp xác định hướng vuông góc với các mặt phẳng hoặc đường thẳng. Việc nắm vững kiến thức và cách tính vecto pháp tuyến sẽ hỗ trợ bạn giải quyết nhiều bài toán hình học một cách hiệu quả. Hãy cùng khám phá những ứng dụng và phương pháp liên quan trong bài viết này.

Vecto pháp tuyến là gì?

Vecto pháp tuyến là một vecto vuông góc với mặt phẳng tiếp xúc hoặc đường tiếp xúc tại một điểm. Vecto này có hướng thẳng đứng với bề mặt và được sử dụng rộng rãi trong hình học, vật lý và các ứng dụng kỹ thuật.

Trong không gian ba chiều, vecto pháp tuyến đóng vai trò quan trọng trong việc xác định hướng của một mặt phẳng. Nó giúp xác định góc nghiêng của mặt phẳng so với các trục tọa độ và được sử dụng để tính toán các đại lượng như lực, moment và các tham số vật lý khác tác động lên bề mặt.

Một ứng dụng điển hình của vecto pháp tuyến là trong công nghệ đồ họa máy tính và thiết kế 3D. Các phần mềm thiết kế như AutoCAD và 3DS Max sử dụng vecto pháp tuyến để tính toán ánh sáng, bóng đổ và độ phản xạ của các bề mặt, tạo nên hình ảnh chân thực và sống động.

Trong lĩnh vực xây dựng và kiến trúc, vecto pháp tuyến giúp kỹ sư và kiến trúc sư tính toán lực tác động lên các cấu trúc, đảm bảo độ bền và an toàn cho công trình. Ví dụ, khi thiết kế mái nhà, vecto pháp tuyến được sử dụng để tính toán phân bố lực của gió và tải trọng tuyết, từ đó xác định độ dốc và vật liệu phù hợp.

Đặc điểm và tính chất cơ bản của vecto pháp tuyến trong hình học

Vecto pháp tuyến là một khái niệm quan trọng trong hình học, đại diện cho vecto vuông góc với một đường thẳng hoặc mặt phẳng tại một điểm. Tương tự như cách biểu đồ venn là gì giúp biểu diễn mối quan hệ giữa các tập hợp, vectơ pháp tuyến giúp xác định hướng vuông góc với một đối tượng hình học.

Trong không gian ba chiều, vecto pháp tuyến đóng vai trò then chốt trong việc xác định phương trình mặt phẳng và tính toán góc giữa các mặt phẳng. Tính chất vectơ pháp tuyến thể hiện rõ nhất qua khả năng xác định độ nghiêng của mặt phẳng và hướng vuông góc với mặt phẳng đó.

Khái niệm về vecto pháp tuyến của đường thẳng và mặt phẳng

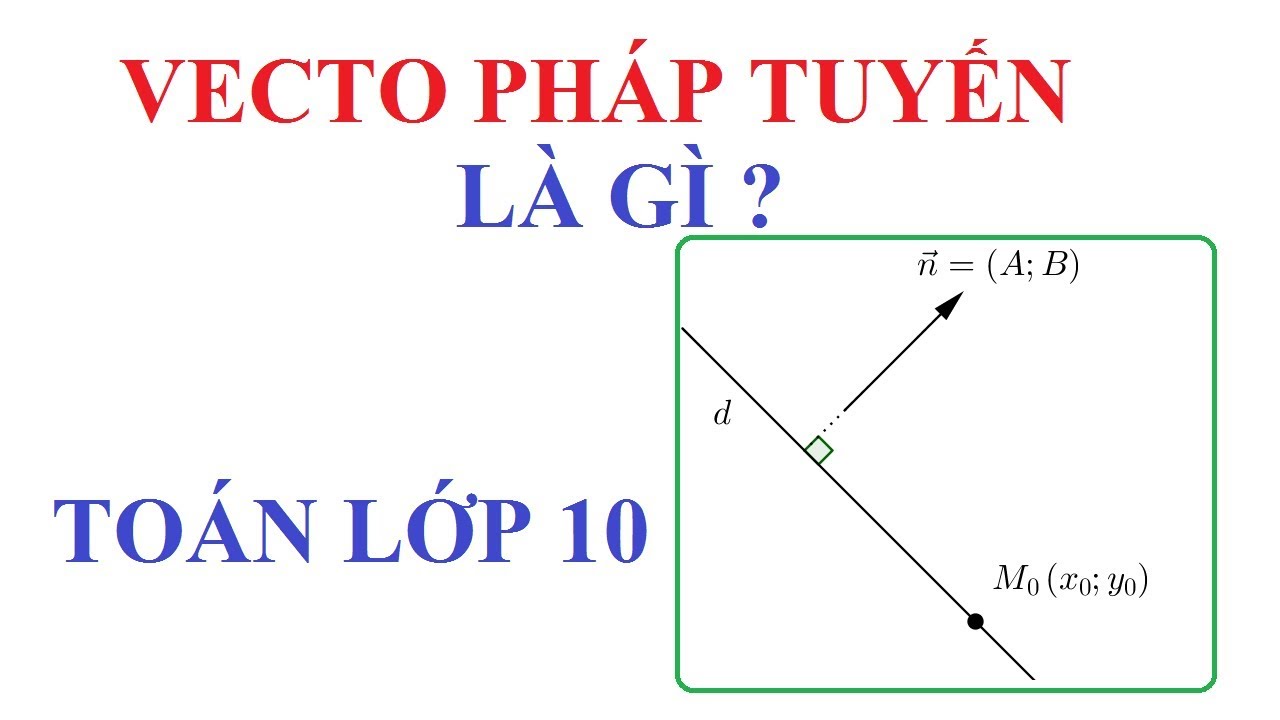
Vecto pháp tuyến của đường thẳng là vecto vuông góc với đường thẳng tại một điểm. Trong mặt phẳng, nếu đường thẳng có phương trình ax + by + c = 0, thì vecto n = (a,b) chính là vecto pháp tuyến của đường thẳng đó.

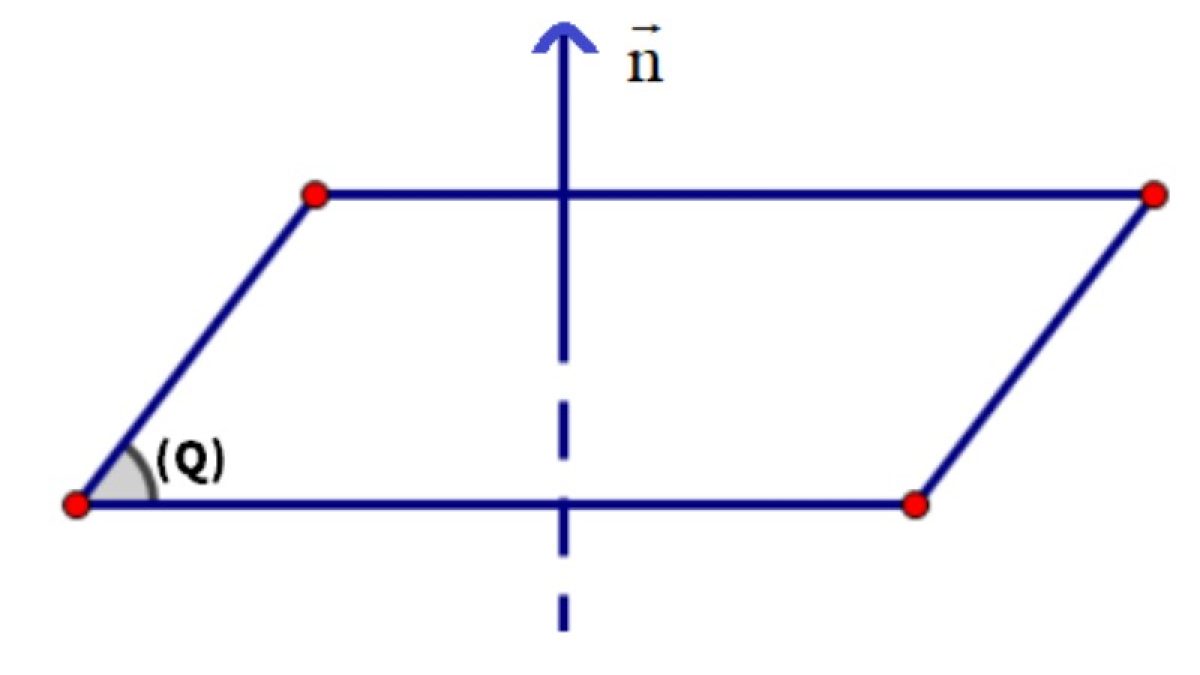
Đối với mặt phẳng trong không gian ba chiều, vecto pháp tuyến là vecto vuông góc với mọi đường thẳng nằm trên mặt phẳng đó. Với mặt phẳng có phương trình ax + by + cz + d = 0, vecto n = (a,b,c) là vecto pháp tuyến của mặt phẳng.

Các tính chất quan trọng của vecto pháp tuyến

Vecto pháp tuyến có tính chất đối xứng, nghĩa là nếu n là vecto pháp tuyến thì -n cũng là vecto pháp tuyến của cùng một đối tượng hình học. Điều này cho phép linh hoạt trong việc lựa chọn hướng của vecto pháp tuyến.

Độ dài của vecto pháp tuyến không ảnh hưởng đến tính chất vuông góc của nó. Hai vecto pháp tuyến của cùng một đối tượng hình học luôn cùng phương, chỉ có thể khác về độ dài hoặc hướng.

Tích vô hướng của vecto pháp tuyến với bất kỳ vecto nào nằm trên đường thẳng hoặc mặt phẳng luôn bằng 0, thể hiện tính chất vuông góc giữa chúng.

Mối quan hệ giữa vecto pháp tuyến và vecto chỉ phương

Vecto pháp tuyến và vecto chỉ phương luôn vuông góc với nhau. Trong không gian hai chiều, nếu u = (a,b) là vecto chỉ phương của đường thẳng, thì n = (-b,a) là một vecto pháp tuyến của đường thẳng đó.

Khi biết vecto chỉ phương, ta có thể dễ dàng xác định vecto pháp tuyến bằng cách đổi vị trí các thành phần và đổi dấu một trong hai thành phần. Ngược lại, từ vecto pháp tuyến cũng có thể xác định được vecto chỉ phương theo nguyên tắc tương tự.

Trong thực tế, mối quan hệ này được ứng dụng rộng rãi trong thiết kế công trình, tính toán lực tác động và nhiều lĩnh vực kỹ thuật khác.

Phương pháp xác định và tính toán vecto pháp tuyến

Vecto pháp tuyến đóng vai trò quan trọng trong hình học không gian và các ứng dụng thực tế. Để xác định và tính toán vecto pháp tuyến một cách chính xác, cần nắm vững các phương pháp và công thức cơ bản. Việc tính toán vectơ trong không gian đòi hỏi sự tỉ mỉ và tuân thủ các quy tắc toán học.

Trước khi đi sâu vào các phương pháp cụ thể, cần hiểu rằng vecto pháp tuyến luôn vuông góc với mặt phẳng hoặc đường thẳng tại điểm đang xét. Điều này có mối liên hệ chặt chẽ với cát tuyến là gì, giúp xác định hướng của vecto một cách chính xác.

Cách xác định vecto pháp tuyến từ phương trình mặt phẳng

Khi có phương trình mặt phẳng ax + by + cz + d = 0, vecto pháp tuyến được xác định bởi các hệ số của x, y và z. Vecto n = (a,b,c) chính là vecto pháp tuyến của mặt phẳng đó.

Phương pháp này áp dụng cho mọi dạng phương trình mặt phẳng, kể cả khi phương trình ở dạng tổng quát hay tham số. Cách xác định vecto pháp tuyến từ phương trình mặt phẳng là cơ sở để giải quyết nhiều bài toán hình học không gian.

Công thức tính vecto pháp tuyến của đường thẳng

Đối với đường thẳng trong mặt phẳng, vecto pháp tuyến có thể tính được thông qua phương trình đường thẳng ax + by + c = 0. Vecto pháp tuyến sẽ có dạng n = (a,b).

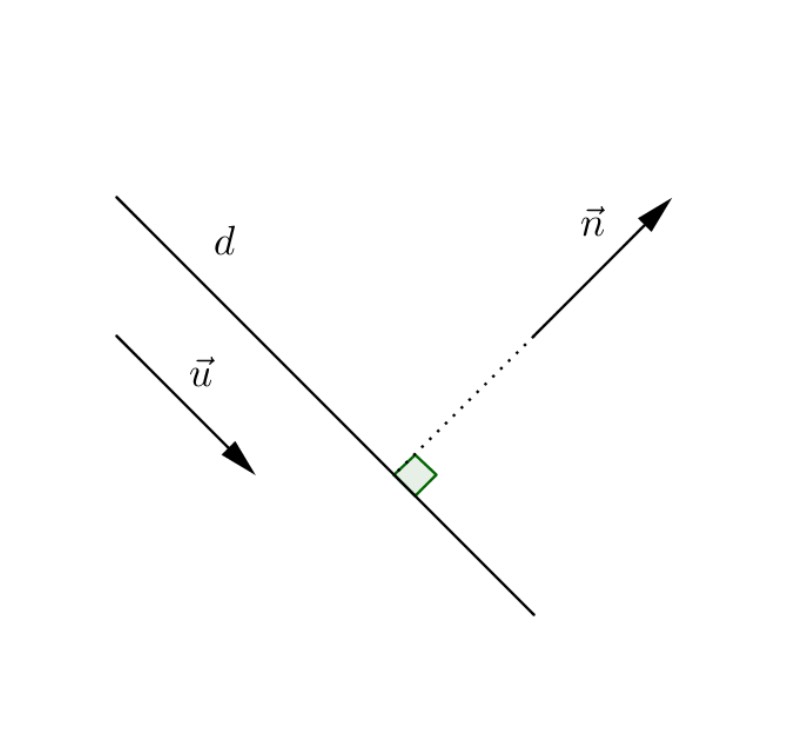
Công thức tính vecto pháp tuyến còn có thể áp dụng cho trường hợp đường thẳng được cho bởi hai điểm A(x₁,y₁) và B(x₂,y₂). Khi đó, nếu vecto chỉ phương của đường thẳng là v = (x₂-x₁, y₂-y₁), thì vecto pháp tuyến sẽ là n = (-(y₂-y₁), x₂-x₁).

Các bước tính vecto pháp tuyến trong không gian ba chiều

Bước 1: Xác định dạng của đối tượng hình học (mặt phẳng, đường thẳng hay mặt cong)
Bước 2: Chuyển đổi phương trình về dạng chuẩn nếu cần thiết
Bước 3: Áp dụng công thức tương ứng với từng trường hợp
Bước 4: Kiểm tra tính vuông góc của vecto pháp tuyến với đối tượng hình học

Việc tuân thủ các bước này giúp đảm bảo kết quả chính xác và tránh các sai sót trong quá trình tính toán. Đặc biệt với các bài toán phức tạp, việc thực hiện theo trình tự sẽ giúp giải quyết vấn đề một cách có hệ thống.

Ứng dụng của vecto pháp tuyến trong giải toán hình học

Vecto pháp tuyến là một công cụ toán học quan trọng giúp giải quyết nhiều bài toán hình học phức tạp. Với đặc điểm luôn vuông góc với mặt phẳng tại một điểm, vecto này giúp xác định phương trình mặt phẳng và tính toán các yếu tố hình học liên quan.

Việc áp dụng ứng dụng vectơ pháp tuyến mang lại hiệu quả cao trong việc giải các bài toán về góc, khoảng cách và vị trí tương đối giữa các đối tượng hình học. Website về môn toán cung cấp nhiều ví dụ minh họa cụ thể về cách sử dụng vecto pháp tuyến.

Sử dụng vecto pháp tuyến để tìm phương trình mặt phẳng

Khi biết một điểm thuộc mặt phẳng và vecto pháp tuyến của mặt phẳng đó, ta có thể xác định được phương trình mặt phẳng một cách dễ dàng. Phương pháp vectơ này dựa trên tính chất vecto pháp tuyến vuông góc với mọi vecto nằm trong mặt phẳng.

Ví dụ thực tế từ GS. Nguyễn Văn A – Đại học Bách Khoa Hà Nội: “Trong thiết kế công trình, việc xác định phương trình mặt phẳng mái dốc thông qua vecto pháp tuyến giúp tính toán chính xác góc nghiêng và diện tích bề mặt.”

Xác định góc giữa hai mặt phẳng bằng vecto pháp tuyến

Góc giữa hai mặt phẳng chính là góc giữa hai vecto pháp tuyến của chúng. Phương pháp này đơn giản hóa việc tính toán góc giữa các mặt phẳng phức tạp trong không gian ba chiều.

Trong thực tế, kỹ sư xây dựng thường sử dụng nguyên lý này để tính toán độ nghiêng giữa các mặt của công trình, đảm bảo tính thẩm mỹ và an toàn kết cấu.

Việc áp dụng công thức cos của góc giữa hai vecto kết hợp với vecto pháp tuyến cho phép xác định chính xác góc giữa hai mặt phẳng bất kỳ.

Giải các bài toán về khoảng cách điểm đến mặt phẳng

Khoảng cách từ một điểm đến mặt phẳng được tính thông qua vecto pháp tuyến của mặt phẳng đó. Công thức tính khoảng cách này có ý nghĩa quan trọng trong nhiều ứng dụng thực tiễn.

Trong ngành công nghiệp sản xuất, việc tính toán khoảng cách từ các cảm biến đến bề mặt sản phẩm giúp kiểm soát chất lượng và độ chính xác của quy trình sản xuất.

Phương pháp này còn được ứng dụng trong công nghệ thực tế ảo để xác định va chạm giữa các vật thể trong không gian ba chiều, tạo nên trải nghiệm chân thực cho người dùng.

Các dạng bài tập thường gặp về vecto pháp tuyến

Để giải quyết các bài toán liên quan đến vecto pháp tuyến là gì, cần nắm vững các dạng bài tập cơ bản và phương pháp giải phù hợp. Các dạng bài tập này thường xuất hiện trong chương trình hình học không gian và đòi hỏi kỹ năng tính toán chính xác.

Việc tính vecto pháp tuyến đóng vai trò quan trọng trong việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng. Thông qua các bài tập điển hình, học sinh sẽ rèn luyện được kỹ năng vận dụng kiến thức một cách linh hoạt và hiệu quả.

Bài tập về tìm vecto pháp tuyến của mặt phẳng

Khi giải các bài toán về vecto pháp tuyến của mặt phẳng, cần xác định rõ phương trình mặt phẳng dưới dạng tổng quát ax + by + cz + d = 0. Từ đó, vecto pháp tuyến sẽ có dạng n = (a,b,c).

Một số phương pháp tìm vecto pháp tuyến thường được áp dụng như: sử dụng tích có hướng của hai vecto chỉ phương nằm trên mặt phẳng, hoặc dựa vào hệ số của phương trình mặt phẳng. Việc nắm vững các phương pháp này giúp giải quyết nhanh chóng nhiều dạng bài tập khác nhau.

Bài tập về góc giữa đường thẳng và mặt phẳng

Góc giữa đường thẳng và mặt phẳng được xác định thông qua công thức sin α = |n.v|/(|n|.|v|), trong đó n là vecto pháp tuyến của mặt phẳng và v là vecto chỉ phương của đường thẳng. Hướng dẫn vectơ pháp tuyến cần chú ý đến dấu của các thành phần vecto.

Việc tính góc giữa đường thẳng và mặt phẳng thường đòi hỏi kỹ năng biến đổi đại số và sử dụng các công thức lượng giác. Cần kiểm tra kỹ các bước tính để tránh sai sót trong quá trình giải.

Bài tập tổng hợp và phương pháp giải

Các bài tập tổng hợp thường kết hợp nhiều kiến thức về vecto pháp tuyến, góc, khoảng cách và vị trí tương đối. Phương pháp giải cần theo các bước:

• Xác định dữ kiện và yêu cầu bài toán
• Chọn hệ trục tọa độ phù hợp
• Thiết lập các phương trình và biểu thức cần thiết
• Áp dụng công thức và tính toán
• Kiểm tra kết quả và kết luận

Việc giải bài tập tổng hợp đòi hỏi tư duy logic và khả năng phân tích vấn đề toàn diện. Thông qua việc luyện tập nhiều dạng bài khác nhau, học sinh sẽ nâng cao được kỹ năng giải toán hình học không gian.

Vecto pháp tuyến là gì? Đây chính là yếu tố quan trọng trong hình học, giúp xác định hướng và giải quyết nhiều bài toán liên quan đến đường thẳng và mặt phẳng. Việc nắm vững các khái niệm, tính chất cùng phương pháp tính vecto pháp tuyến sẽ hỗ trợ bạn giải quyết hiệu quả các bài tập trong chương trình học. Hãy áp dụng những kiến thức này vào thực tiễn để nâng cao khả năng toán học của mình.