Diện tích hình lập phương là một nội dung quan trọng trong toán học. Bởi vì việc tính các hình sẽ sử dụng rất nhiều tới công thức tính diện tích. Cho nên, các bạn sẽ phải ghi nhớ được từng công thức cụ thể, đảm bảo được kết quả tính toán đúng.
Diện tích hình lập phương là gì?
Hình lập phương là một khối hình học với các cạnh đều bằng nhau và mỗi mặt là hình vuông. Diện tích của hình lập phương là một công thức tính kích thước trong toán học.
Các bạn sẽ thấy diện tích khối lập phương có rất nhiều công thức. Ví dụ như tích S đáy, S toàn phần và S bề mặt. Mỗi công thức sẽ được dùng trong nhiều trường hợp khác nhau. Ngoài ra để tính được một bài tính hình lập phương hoàn chỉnh, bạn cần phải học và ghi nhớ đúng từng chi tiết.
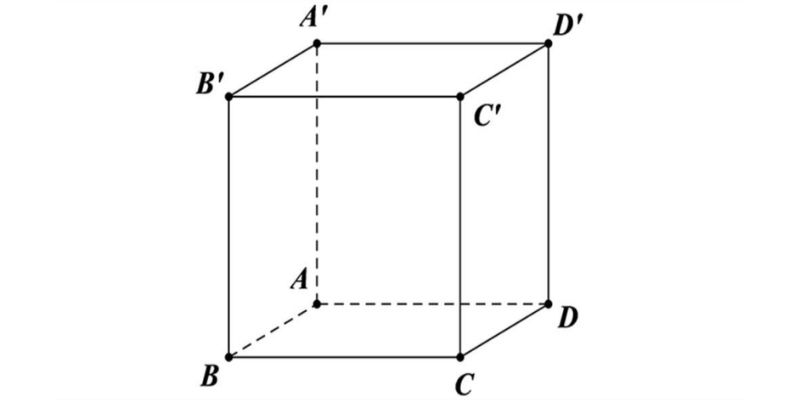 Những loại diện tích trong hình lập phương
Những loại diện tích trong hình lập phương
Trong toán học, diện tích khối lập phương được chia thành nhiều loại. Mỗi diện tích sẽ được tính bằng công thức khác nhau. Các bạn cần lưu ý ghi nhớ chính xác để tránh nhầm lẫn khi thực hiện phép tính.
Diện tích toàn phần hình lập phương
Diện tích toàn phần của hình lập phương là tổng diện tích của tất cả 6 mặt bên. Công thức tính S toàn phần hình lập phương này giúp đo lường kích thước bề mặt cũng như chứng minh khả năng của hình bao phủ được không gian nhất định.
- S toàn phần giúp bạn tính toán được số lượng vật liệu cần dùng để tạo ra một vật thể hoặc bề mặt nào đó.
- Trong hình học không gian, diện tích toàn phần cung cấp cái nhìn tổng quan và đầy đủ về kích thước bề mặt của hình đó, giúp cho việc tính toán chu vi hình lập phương và thiết kế trở nên chính xác hơn.
Công thức tính diện tích toàn phần tương đối đơn giản. Các bạn khi học chứng minh hình không gian đều có thể áp dụng vào thực tiễn.
Công thức diện tích toàn phần là:
$$Stp=6\times a^2$$
Trong đó
- a là độ dài cạnh của hình
- Stp là diện tích toàn phần.
Ví dụ dễ hiểu: Xét hình lập phương có cạnh là 4 cm. Khi đó $$Stp=6\times42=96cm2$$
Khi tính toán S toàn phần, các bạn cần phải lưu ý một vài điều để tránh nhầm lẫn:
- Độ dài cạnh của hình cần được đo hoàn toàn chuẩn.
- Công thức cần phải áp dụng đúng để không bị tính toán sai.
- Diện tích toàn phần còn phản ánh cả diện tích các mặt gồm mặt đáy và mặt bên.
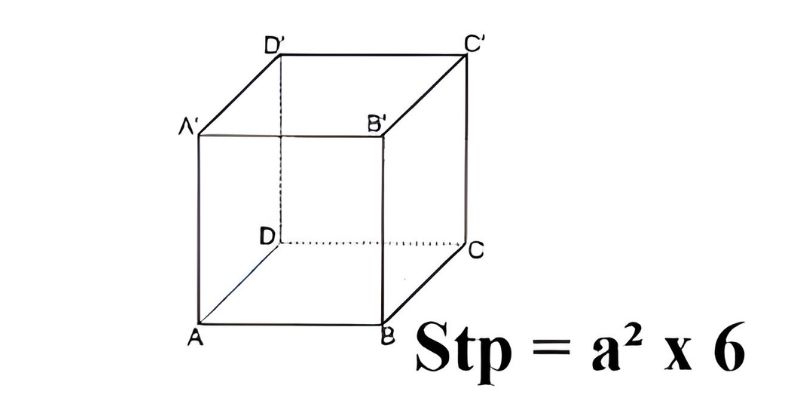 Diện tích xung quanh hình lập phương
Diện tích xung quanh hình lập phương
Diện tích xung quanh của hình lập phương được hiểu là diện tích một mặt nhân 4. Các bạn không nên nhầm lẫn công thức này với S diện tích toàn phần. Có khá nhiều bạn khi mới bắt đầu tiếp cận công thức rất dễ nhầm nên phải ghi nhớ cẩn thận.
Công thức tính của Sxq hình lập phương:
$$Sxq=a\times a\times4$$
Ví dụ: Các bạn tính diện tích xung quanh hình lập phương với cạnh 10cm. Kết quả đưa ra là Sxq = 10 x 10 x 4 = 400 cm2.
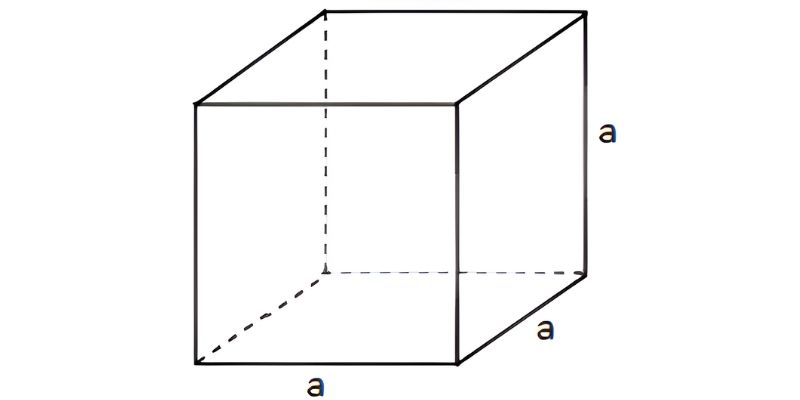 Diện tích bề mặt hình lập phương
Diện tích bề mặt hình lập phương
Diện tích khối lập phương theo bề mặt vật thể là công thức tính tổng diện tích bề mặt có trên vật thể. Bởi vì khối lập phương nào cũng có 6 mặt nên S sẽ tính bằng 1 mặt nhân với 6.
Cách tính S bề mặt của hình lập phương
$$Sbm=6\times a^2$$
Ví dụ là tính S bề mặt của hình lập phương với cạnh dài 3 cm. Kết quả khi đó là Sbm = 6 x 3 x 3 = 54 cm2.
Những ứng dụng của công thức diện tích khối lập phương
Việc tính được diện tích khối lập phương là một kỹ năng không chỉ dùng để chứng minh các bài toán. Mà bên cạnh đó, bạn có thể áp dụng rộng rãi vào thực tiễn. Ở một số ngành nghề, các bạn khi biết rõ công thức tính S lập phương vô cùng có lợi.
- Trong hoạt động giáo dục: Với 1 trong các công thức tính diện tích hình lập phương kể trên, bạn hoàn toàn có thể tìm ra độ dài cạnh của hình lập phương, từ đó áp dụng công thức và tính toán thể tích hình lập phương. Ngoài ra, việc nắm chắc công thức còn giúp bạn dễ dàng làm các bài tập chứng mình hình học khác.
- Trong thiết kế và xây dựng không gian: Việc tính S hình lập phương cực kỳ sát với các công trình xây dựng và thiết kế, giúp bạn ước lượng được số vật liệu cần sử dụng.
- Tối ưu được khoản chi phí: Các bạn khi tính toán chính xác có thể tối ưu được phần nào chi phí cần phải bỏ ra khi tiến hành chọn lựa vật liệu. Tất nhiên việc tính toán này sẽ mang lại hiệu quả cao hơn khi chỉ dựa vào mắt nhìn.
Chu vi khối lập phương là gì?
Hình lập phương là khối đa diện đều, bao gồm tổng 6 mặt hình vuông, 12 cạnh và 8 đỉnh. Bạn có thể hiểu một cách đơn giản nhất là 1 hình khối mang chiều rộng, chiều dài, chiều cao đều bằng nhau.
Tính chất cơ bản của 1 khối lập phương dễ dàng nhận biết. Gồm có:
- 8 mặt phẳng đối xứng nhau.
- 12 cạnh đều, 8 đỉnh và 3 cạnh gặp nhau sẽ tạo thành 1 đỉnh.
- 4 đường chéo cắt nhau tại 1 điểm, điểm này được xem như tâm đối xứng của hình lập phương.
- Các đường chéo ở mặt bên và độ dài chúng đều bằng nhau.
Bằng mắt thường, bạn có thể nhanh chóng nhận ra hình lập phương thông qua 2 đặc điểm nổi bật sau:
- Có 12 cạnh bằng nhau.
- Tất cả 6 mặt đều là hình vuông.
Công thức tính chu vi hình lập phương chuẩn xác
Bạn cần ghi nhớ thật chính xác cách tính chu vi để tránh nhầm lẫn qua lại các công thức với nhau trong quá trình diễn ra tính toán.
Tính chu vi của khối lập phương
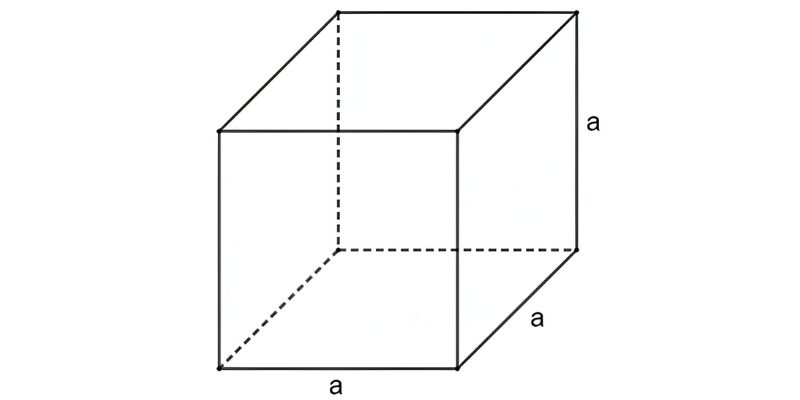
Chu vi khối lập phương là tổng độ dài của toàn bộ các cạnh. Mỗi hình lập phương có 12 cạnh với độ dài đều bằng nhau. Để tính chu vi tổng khối, bạn chỉ cần nhân độ dài của 1 cạnh với 12, vì hình 1 hình lập phương có tổng cộng 12 cạnh.
Công thức tính như sau:
Trong đó:
- P: tổng chu vi khối lập phương.
- a: độ dài của 1 cạnh khối lập phương.
Một ví dụ minh họa vô cùng dễ hiểu như sau: Tính chu vi khối lập phương có độ dài 1 cạnh là 6 cm. Áp dụng công thức ở trên, bạn được: P = 12 x 6 = 72 (cm).
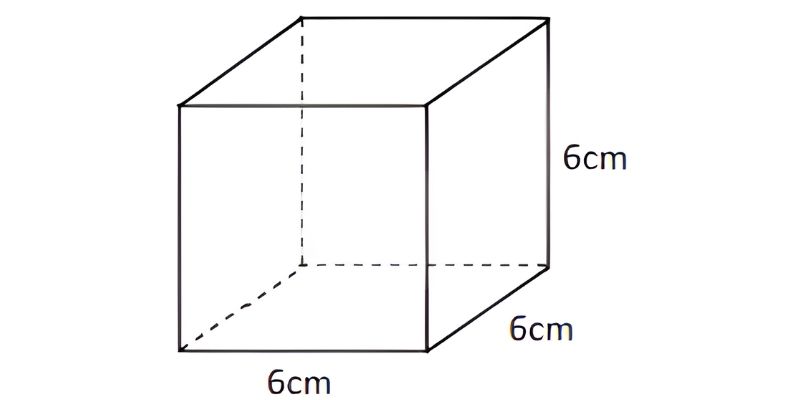
Công thức chu vi đáy hình lập phương
Chu vi mặt đáy của 1 khối lập phương chính là chu vi của hình vuông hay còn gọi là tổng độ dài 4 cạnh của mặt đáy hình vuông đó. Bạn chỉ cần lấy độ dài 1 cạnh nhân với 4 là ra kết quả.
Ta có công thức tính chu vi đáy hình lập phương như sau:
Trong đó:
- Pđáy là chu vi đáy của hình lập phương.
- a là độ dài 1 cạnh hình vuông trong khối lập phương.
Một ví dụ giúp bạn dễ hiểu hơn về công thức này:
Giả sử 1 khối lập phương có độ dài các cạnh là 8 cm. Hãy tính chu vi đáy bằng cách bạn áp dụng công thức cung cấp ở trên vào, ta được: Pđáy= 4 X 8 = 32 (cm).
Ứng dụng trong đời sống
Không chỉ được sử dụng để tính toán thế tich khối lập phương, công thức tính chu vi khối lập phương còn có công dụng hữu ích trong đời sống thực tiễn. Ở một số ngành, khi bạn đã nắm chắc trong đầu những công thức sẽ được áp dụng như sau:
- Thiết kế & sản xuất đồ chơi: Khi lên ý tưởng sáng tạo, thiết kế các hình lập phương làm những món đồ chơi cho trẻ em. Nhà sản xuất cần phải biết chính xác kích thước của hình để đảm bảo sản phẩm đưa ra phù hợp với tiêu chuẩn thị trường.
- Đóng gói & vận chuyển:
Trong quá trình đóng gói bất kì sản phẩm nào có cấu trúc hình lập phương, biết được cách tính chu vi sẽ giúp bạn tính toán đúng kích thước hộp đựng.
Điều này tạo nên sự tiết kiệm, tối ưu hóa chi phí vận chuyển, sản phẩm không bị hư hỏng do sai kích thước.
- Giáo dục: Bên cạnh thể tích, từ chu vi của hình lập phương, áp dụng công thức, chúng ta có thể biết được độ dài cạnh và tính được diện tích hình lập phương.
- Trong công nghiệp: Việc tính chu vi khối lập phương được các nhà sản xuất đưa vào quyết định kích thước của những bộ phận máy móc, hỗ trợ tạo ra những linh kiện cho thiết bị.
- Kiến trúc & xây dựng: Các kiến trúc sư tận dụng công thức vào thiết kiết không gian nhà, phòng ốc,…Bên cạnh đó, tính toán chu vi giúp nhiều kỹ sư xác định kích thước nguyên vật liệu.
Kết luận
Công thức tính diện tích hình lập phương được nêu một cách đầy đủ và chi tiết ở phần trên. Hầu hết các công thức đều không khó, Luyện tập nhiều sẽ giúp bạn dễ dàng áp dụng công thức này vào học tập cũng như trong cuộc sống thực tế.




