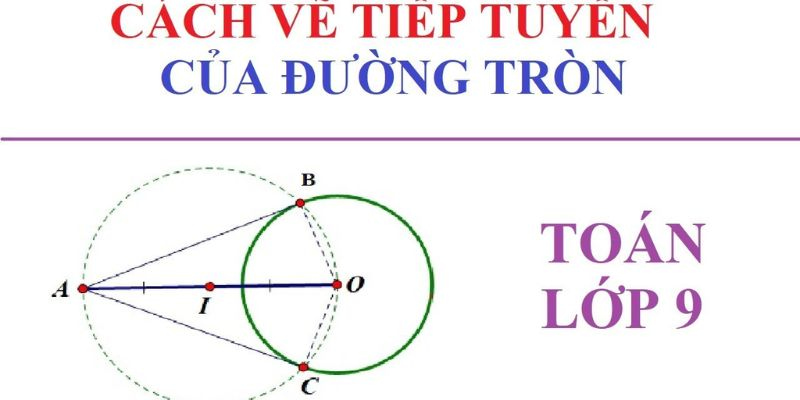
Phương trình tiếp tuyến: công thức, cách viết và ứng dụng trong toán học

Phương trình tiếp tuyến là một khái niệm quan trọng trong hình học giải tích. Để tìm phương trình tiếp tuyến của đồ thị hàm số, bạn cần nắm rõ các công thức và quy trình xác định. Bài viết này sẽ hướng dẫn bạn cách viết phương trình tiếp tuyến và áp dụng các công thức liên quan. Hãy cùng khám phá và trau dồi kỹ năng toán học của bạn!

Phương trình tiếp tuyến và các khái niệm cơ bản trong hình học giải tích

Phương trình tiếp tuyến là phương trình của đường thẳng tiếp xúc với một đường cong tại một điểm. Đây là một công cụ quan trọng trong phương trình đường thẳng và hình học giải tích, giúp xác định độ dốc cũng như hướng của đường cong tại một điểm cụ thể.

Khi nghiên cứu về pttt là gì, ta cần hiểu rằng nó thể hiện mối quan hệ giữa đường thẳng tiếp xúc và đường cong tại điểm tiếp xúc. Tại điểm này, đường thẳng tiếp tuyến có cùng hệ số góc (độ dốc) với đường cong, giúp mô tả sự biến thiên của hàm số tại điểm đó một cách chính xác.

Để tìm phương trình tiếp tuyến, việc áp dụng toạ độ hóa là phương pháp hiệu quả. Phương pháp này cho phép chuyển đổi các bài toán hình học sang dạng đại số, từ đó dễ dàng xác định được phương trình tiếp tuyến thông qua việc tính đạo hàm và sử dụng các công thức tương ứng.

Trong thực tế, phương trình tiếp tuyến có nhiều ứng dụng quan trọng trong kỹ thuật và khoa học. Ví dụ, khi thiết kế đường cong khí động học cho máy bay, các kỹ sư sử dụng phương trình tiếp tuyến để tối ưu hóa hình dạng cánh máy bay, giúp giảm lực cản không khí và tăng hiệu suất bay.

Công thức tổng quát và cách xác định phương trình tiếp tuyến của đồ thị hàm số

Phương trình tiếp tuyến là một công cụ quan trọng trong việc nghiên cứu tính chất hình học của đồ thị hàm số. Việc nắm vững công thức phương trình tiếp tuyến giúp giải quyết nhiều bài toán phức tạp trong giải tích và hình học vi phân.

Công thức tổng quát của phương trình tiếp tuyến

Phương trình tiếp tuyến có dạng y – y₀ = k(x – x₀), trong đó (x₀,y₀) là tọa độ điểm tiếp xúc và k là hệ số góc của tiếp tuyến. Với hàm số y = f(x) khả vi tại x₀, hệ số góc k chính là đạo hàm của hàm số tại điểm tiếp xúc: k = f'(x₀).

Khi áp dụng vào thực tế, công thức pt tiếp tuyến thường được viết dưới dạng: y = f'(x₀)(x – x₀) + f(x₀). Công thức này có ý nghĩa hình học sâu sắc và được ứng dụng rộng rãi trong nhiều lĩnh vực khoa học kỹ thuật.

Các bước xác định phương trình tiếp tuyến tại một điểm

Bước đầu tiên là xác định tọa độ điểm tiếp xúc (x₀,y₀) trên đồ thị hàm số. Điểm này phải thỏa mãn điều kiện y₀ = f(x₀).

Tiếp theo, tính đạo hàm f'(x) của hàm số và xác định giá trị f'(x₀) tại điểm tiếp xúc. Đây chính là hệ số góc của tiếp tuyến.

Cuối cùng, thay các giá trị đã tìm được vào công thức tổng quát để thu được phương trình tiếp tuyến cần tìm. Quá trình này đòi hỏi sự cẩn thận và chính xác trong tính toán.

Ý nghĩa hình học của hệ số góc tiếp tuyến

Hệ số góc tiếp tuyến thể hiện độ dốc của đường cong tại điểm tiếp xúc. Giá trị dương cho biết đồ thị đang tăng, giá trị âm cho thấy đồ thị đang giảm tại điểm đang xét.

Trong nghiên cứu về tốc độ biến thiên, hệ số góc tiếp tuyến còn phản ánh tốc độ thay đổi tức thời của đại lượng. Ví dụ, trong vật lý, hệ số góc tiếp tuyến của đồ thị quãng đường-thời gian chính là vận tốc tức thời của vật.

Ngoài ra, hệ số góc tiếp tuyến còn giúp xác định các cực trị địa phương của hàm số khi nó bằng 0, và điểm uốn khi nó đổi dấu.

Phương pháp viết phương trình tiếp tuyến trong các dạng bài tập điển hình

Cách viết phương trình tiếp tuyến đóng vai trò quan trọng trong việc giải các bài toán hình học giải tích. Để nắm vững phương pháp này, cần hiểu rõ mệnh đề kéo theo giữa điều kiện tiếp xúc và phương trình tiếp tuyến. Việc xác định phương trình tiếp tuyến thường được chia thành 3 dạng chính dựa vào điều kiện đã biết.

Viết phương trình tiếp tuyến khi biết tọa độ điểm tiếp xúc

Khi biết tọa độ điểm tiếp xúc, ta có thể áp dụng công thức tổng quát để viết pt tiếp tuyến. Đầu tiên, xác định đạo hàm của hàm số tại điểm tiếp xúc để tìm hệ số góc của tiếp tuyến. Sau đó, thay tọa độ điểm tiếp xúc và hệ số góc vào phương trình đường thẳng y – y0 = k(x – x0).

Phương pháp này đặc biệt hiệu quả khi làm việc với các đường cong bậc hai như parabol, hypecbol. Việc xác định chính xác tọa độ điểm tiếp xúc giúp ta tránh được nhiều sai sót trong quá trình tính toán.

Viết phương trình tiếp tuyến song song hoặc vuông góc với đường thẳng cho trước

Đối với dạng bài này, ta cần dựa vào mối quan hệ giữa các hệ số góc. Nếu hai đường thẳng song song, chúng có cùng hệ số góc. Nếu hai đường thẳng vuông góc, tích hai hệ số góc bằng -1.

Sau khi xác định được hệ số góc của tiếp tuyến cần tìm, ta sử dụng điều kiện tiếp xúc để thiết lập hệ phương trình. Việc giải hệ phương trình này sẽ cho ta tọa độ điểm tiếp xúc, từ đó xác định được phương trình tiếp tuyến cần tìm.

Viết phương trình tiếp tuyến có hệ số góc cho trước

Khi đã biết hệ số góc của tiếp tuyến, ta có thể áp dụng viết phương trình tiếp tuyến theo các bước sau:

• Thiết lập phương trình tiếp tuyến dạng y = kx + b với k là hệ số góc đã cho
• Tìm tọa độ điểm tiếp xúc bằng cách giải hệ phương trình từ điều kiện tiếp xúc
• Thay tọa độ điểm tiếp xúc vào phương trình để tìm b

Phương pháp này thường được áp dụng hiệu quả cho các đường cong đơn giản như parabol hay đường tròn. Việc biết trước hệ số góc giúp đơn giản hóa quá trình tính toán đáng kể.

Ứng dụng đạo hàm trong việc tìm phương trình tiếp tuyến

Đạo hàm đóng vai trò quan trọng trong việc xác định phương trình tiếp tuyến của đường cong tại một điểm. Khi giải quyết các bài toán liên quan đến phương trình tiếp tuyến đạo hàm, việc nắm vững mối quan hệ giữa đạo hàm và hệ số góc tiếp tuyến là yếu tố then chốt.

Trong nhiều trường hợp, việc tìm phương trình tiếp tuyến có thể trở nên phức tạp khi gặp các phương trình vô tỉ hoặc phương trình trùng phương. Tuy nhiên, với sự hỗ trợ của đạo hàm, ta có thể xác định chính xác phương trình tiếp tuyến tại bất kỳ điểm nào trên đường cong.

Mối quan hệ giữa đạo hàm và hệ số góc tiếp tuyến

Đạo hàm tại một điểm chính là hệ số góc của tiếp tuyến tại điểm đó. Điều này tạo nên mối liên hệ trực tiếp giữa đạo hàm và tiếp tuyến của đường cong.

Khi xét một hàm số y = f(x), giá trị đạo hàm f'(x0) tại điểm có hoành độ x0 sẽ cho ta hệ số góc của tiếp tuyến tại điểm đó. Từ đó, ta có thể xây dựng phương trình tiếp tuyến dựa trên dạng y – y0 = k(x – x0), với k là hệ số góc được xác định từ đạo hàm.

Việc hiểu rõ mối quan hệ này giúp ta giải quyết hiệu quả các bài toán về phương trình tiếp tuyến của đạo hàm trong nhiều tình huống khác nhau.

Các trường hợp đặc biệt khi tìm phương trình tiếp tuyến

Một số trường hợp đặc biệt thường gặp khi tìm phương trình tiếp tuyến bao gồm:

• Tiếp tuyến song song với trục hoành: Đạo hàm bằng 0
• Tiếp tuyến song song với trục tung: Đạo hàm không xác định
• Tiếp tuyến tại điểm uốn: Đạo hàm bậc hai bằng 0

Ngoài ra, khi đường cong có dạng phức tạp như hàm hợp, hàm ẩn hay hàm tham số, việc tìm tiếp tuyến đòi hỏi phải áp dụng các quy tắc tính đạo hàm tương ứng. Trong một số trường hợp, ta cần kết hợp nhiều phương pháp khác nhau để xác định chính xác phương trình tiếp tuyến cần tìm.

Phương trình tiếp tuyến trong các hệ tọa độ khác nhau

Phương trình tiếp tuyến của đồ thị hàm số có thể được biểu diễn trong các hệ tọa độ khác nhau, phổ biến nhất là hệ tọa độ Đề-các và hệ tọa độ cực. Mỗi hệ tọa độ sẽ có cách biểu diễn và tính toán riêng, phù hợp với từng bài toán cụ thể.

Việc nắm vững cách xác định tiếp tuyến của đồ thị hàm số trong các hệ tọa độ khác nhau giúp giải quyết nhiều bài toán hình học phức tạp. Đặc biệt khi kết hợp với các công thức tính trung tuyến, ta có thể phân tích sâu hơn về tính chất hình học của đường cong.

Phương trình tiếp tuyến trong hệ tọa độ Đề-các

Trong hệ tọa độ Đề-các, phương trình tiếp tuyến tại một điểm được xác định thông qua đạo hàm của hàm số tại điểm đó. Đạo hàm tại điểm tiếp xúc chính là hệ số góc của tiếp tuyến.

Khi xét một điểm M(x0, y0) trên đồ thị hàm số y = f(x), phương trình tiếp tuyến có dạng: y – y0 = f'(x0)(x – x0). Trong đó f'(x0) là đạo hàm của hàm số tại x = x0. Công thức này áp dụng cho mọi hàm số khả vi tại điểm đang xét.

Việc xác định phương trình tiếp tuyến trong hệ Đề-các thường đơn giản và trực quan hơn so với các hệ tọa độ khác. Điều này giúp giải quyết hiệu quả các bài toán về tiếp tuyến trong không gian hai chiều.

Phương trình tiếp tuyến trong hệ tọa độ cực

Trong hệ tọa độ cực, phương trình tiếp tuyến được xác định thông qua mối quan hệ giữa bán kính vector r và góc θ. Việc tính toán phức tạp hơn do cần chuyển đổi giữa các hệ tọa độ.

Nếu đường cong có phương trình r = f(θ), tiếp tuyến tại điểm M(r0, θ0) được xác định qua công thức: r = r0 + f'(θ0)(θ – θ0). Trong đó f'(θ0) là đạo hàm của hàm f(θ) tại θ = θ0.

Phương trình tiếp tuyến trong hệ tọa độ cực đặc biệt hữu ích khi nghiên cứu các đường cong có tính đối xứng tâm hoặc các đường xoắn ốc. Tuy nhiên, việc tính toán thường phức tạp hơn và đòi hỏi kỹ năng chuyển đổi giữa các hệ tọa độ một cách linh hoạt.

Trong lĩnh vực toán học, phương trình tiếp tuyến vừa mang tính lý thuyết vừa có ứng dụng thực tiễn quan trọng. Bài viết đã cung cấp công thức và quy trình viết phương trình tiếp tuyến cho đồ thị hàm số một cách rõ ràng. Hiểu rõ và sử dụng thành thạo các kiến thức này sẽ giúp học sinh giải quyết hiệu quả những bài tập liên quan đến tiếp tuyến, từ đó nâng cao khả năng tính toán và tư duy hình học.