Bất đẳng thức Cauchy Schwarz: Định nghĩa, chứng minh và ứng dụng trong toán học

Bất đẳng thức Cauchy Schwarz là một công cụ quan trọng trong toán học. Bài viết này sẽ giới thiệu về bất đẳng thức Cauchy Schwarz, chứng minh và ứng dụng của nó trong không gian vector. Độc giả sẽ được hướng dẫn chi tiết qua các bài tập, ví dụ cụ thể, giúp nâng cao kỹ năng giải quyết bài toán hiệu quả.

Bất đẳng thức Cauchy Schwarz và ý nghĩa trong toán học

Bất đẳng thức Cauchy Schwarz là một trong những bất đẳng thức quan trọng nhất trong toán học, được phát biểu cho không gian vectơ với tích vô hướng. Bất đẳng thức này khẳng định rằng giá trị tuyệt đối của tích vô hướng của hai vectơ không vượt quá tích của độ dài của chúng.

Trong không gian Euclide, định nghĩa Bất đẳng thức Cauchy Schwarz được thể hiện qua công thức |⟨x,y⟩| ≤ ||x|| ||y||, trong đó ⟨x,y⟩ là tích vô hướng của hai vectơ x và y, ||x|| và ||y|| lần lượt là độ dài của vectơ x và y. Dấu bằng xảy ra khi và chỉ khi hai vectơ x và y cùng phương hoặc ít nhất một trong hai vectơ bằng 0.

Ý nghĩa toán học của bất đẳng thức này rất sâu sắc và rộng rãi. Nó là nền tảng cho nhiều kết quả quan trọng trong giải tích, đại số tuyến tính và lý thuyết xác suất. Trong hình học, bất đẳng thức này giúp chứng minh nhiều mệnh đề về góc giữa các vectơ và khoảng cách giữa các điểm trong không gian. Trong thống kê, nó được sử dụng để thiết lập mối quan hệ giữa phương sai và hiệp phương sai của các biến ngẫu nhiên.

Ứng dụng của bất đẳng thức này còn mở rộng sang nhiều lĩnh vực khác như xử lý tín hiệu, lý thuyết mã hóa và tối ưu hóa. Trong xử lý tín hiệu, nó được sử dụng để thiết kế bộ lọc tối ưu và phân tích tương quan. Trong lý thuyết mã hóa, bất đẳng thức này giúp xác định giới hạn của khả năng sửa lỗi của các mã.

Chứng minh và phát biểu của Bất đẳng thức Cauchy Schwarz

Chứng minh Bất đẳng thức Cauchy Schwarz là một trong những chứng minh quan trọng trong toán học, đặc biệt trong lĩnh vực đại số tuyến tính và giải tích. Bất đẳng thức này có nhiều ứng dụng trong việc giải các bài toán phức tạp và là nền tảng để chứng minh nhiều bất đẳng thức khác như bất đẳng thức am-gm.

Để hiểu rõ hơn về bất đẳng thức này, ta sẽ tìm hiểu phát biểu và các phương pháp chứng minh chính.

Phát biểu bất đẳng thức

Với mọi cặp vector x = (x₁, x₂, …, xₙ) và y = (y₁, y₂, …, yₙ) trong không gian vector n chiều, ta có bất đẳng thức sau:
|(x₁y₁ + x₂y₂ + … + xₙyₙ)|² ≤ (x₁² + x₂² + … + xₙ²)(y₁² + y₂² + … + yₙ²)

Dấu bằng xảy ra khi và chỉ khi hai vector x và y cùng phương, nghĩa là tồn tại số thực k sao cho x = ky.

Các bước chứng minh chi tiết

Bất đẳng thức Cauchy Schwarz có thể được chứng minh bằng nhiều cách khác nhau. Hai phương pháp phổ biến nhất là chứng minh đại số và chứng minh hình học.

Chứng minh đại số

Xét đa thức bậc hai P(t) = (x₁ + ty₁)² + (x₂ + ty₂)² + … + (xₙ + tyₙ)² ≥ 0 với mọi t thuộc R.

Khai triển P(t) ta được:
P(t) = (x₁² + x₂² + … + xₙ²) + 2t(x₁y₁ + x₂y₂ + … + xₙyₙ) + t²(y₁² + y₂² + … + yₙ²)

Do P(t) ≥ 0 với mọi t nên Δ = 4(x₁y₁ + x₂y₂ + … + xₙyₙ)² – 4(x₁² + x₂² + … + xₙ²)(y₁² + y₂² + … + yₙ²) ≤ 0

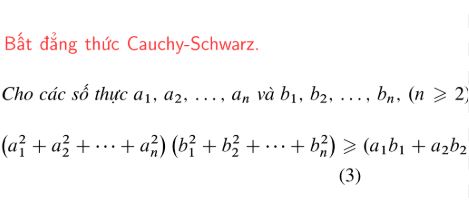
Chứng minh hình học

Phương pháp chứng minh hình học sử dụng khái niệm tích vô hướng và bất đẳng thức tam giác. Xét hai vector a và b trong không gian Euclid, ta có:
|a·b| = |a||b|cosθ ≤ |a||b|

Trong đó θ là góc giữa hai vector. Do |cosθ| ≤ 1 nên |a·b| ≤ |a||b|, và dấu bằng xảy ra khi và chỉ khi hai vector song song.

Ứng dụng Bất đẳng thức Cauchy Schwarz trong không gian vector

Bất đẳng thức Cauchy Schwarz và vector là một công cụ toán học mạnh mẽ, được ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và vật lý. Bất đẳng thức này thiết lập mối quan hệ giữa tích vô hướng của hai vector và tích độ dài của chúng.

Trong không gian vector, bất đẳng thức này giúp chứng minh nhiều mệnh đề quan trọng về hình học và đại số tuyến tính. Nó cũng là nền tảng để phát triển các công cụ tính toán trong Hình học phẳng và không gian ba chiều.

Bất đẳng thức Cauchy Schwarz với tích vô hướng

Trong không gian vector với tích vô hướng, bất đẳng thức Cauchy-Schwarz phát biểu rằng bình phương của tích vô hướng hai vector luôn nhỏ hơn hoặc bằng tích độ dài của chúng. Điều này được biểu diễn qua công thức |⟨x,y⟩|² ≤ ||x||² · ||y||².

Khi áp dụng vào các bài toán cụ thể, bất đẳng thức này giúp ước lượng và so sánh các đại lượng vector một cách hiệu quả. Ví dụ, trong xử lý tín hiệu, nó được sử dụng để tối ưu hóa bộ lọc và nén dữ liệu.

Đặc biệt, dấu bằng xảy ra khi và chỉ khi hai vector tỷ lệ với nhau, tức là một vector là bội số của vector kia. Tính chất này có nhiều ứng dụng trong việc tìm hướng của vector và xác định góc giữa các vector.

Ứng dụng trong không gian Euclid

Trong không gian Euclid, bất đẳng thức Cauchy-Schwarz được áp dụng để giải quyết nhiều bài toán hình học phức tạp. Nó giúp tính toán khoảng cách giữa các điểm, đường thẳng và mặt phẳng một cách chính xác.

Một ứng dụng quan trọng là trong việc tối ưu hóa các bài toán quy hoạch tuyến tính. Theo nghiên cứu của Viện Toán học Việt Nam, bất đẳng thức này được sử dụng rộng rãi trong các thuật toán tối ưu và học máy hiện đại.

Ngoài ra, trong lĩnh vực xử lý ảnh và thị giác máy tính, bất đẳng thức này giúp phân tích các đặc trưng hình học và tính toán độ tương đồng giữa các vector đặc trưng. Điều này đặc biệt hữu ích trong các ứng dụng nhận dạng khuôn mặt và phân tích hình ảnh y tế.

Mối liên hệ giữa Bất đẳng thức Cauchy Schwarz với các bất đẳng thức khác

Bất đẳng thức schwarz có mối liên hệ mật thiết với nhiều bất đẳng thức quan trọng khác trong toán học. Sự kết nối này thể hiện qua việc chúng có thể được suy ra từ nhau hoặc có dạng tương tự nhau trong các không gian khác nhau.

Bất đẳng thức này được xem như một công cụ cơ bản để chứng minh nhiều bất đẳng thức phức tạp hơn. Nó cũng là nền tảng để phát triển các bất đẳng thức mới trong không gian vectơ và không gian Hilbert.

So sánh với bất đẳng thức Bunhiacovski

Bất đẳng thức bunhiacopxki và bất đẳng thức Cauchy-Schwarz thực chất là hai cách phát biểu của cùng một bất đẳng thức trong các không gian khác nhau. Bunhiacovski đưa ra phát biểu trong không gian các hàm liên tục, trong khi Cauchy-Schwarz mở rộng cho không gian vectơ tổng quát.

Sự tương đồng này thể hiện qua cấu trúc toán học và cách áp dụng. Cả hai đều sử dụng tích vô hướng và norm để thiết lập mối quan hệ giữa các đại lượng, tạo nên một công cụ mạnh mẽ trong giải tích toán học.

Liên hệ với bất đẳng thức Cosi

Bất đẳng thức cosi có thể được xem như một trường hợp đặc biệt của bất đẳng thức Cauchy-Schwarz khi áp dụng vào không gian Euclid. Mối liên hệ này thể hiện qua việc bđt schwarz có thể được sử dụng để chứng minh bất đẳng thức cosi một cách trực tiếp.

Trong hình học, bất đẳng thức cosi giúp thiết lập mối quan hệ giữa các cạnh của tam giác, trong khi bất đẳng thức Cauchy-Schwarz mở rộng ý tưởng này ra không gian nhiều chiều. Điều này cho thấy tính phổ quát và sức mạnh của bất đẳng thức Cauchy-Schwarz trong toán học.

Phương pháp giải bài tập sử dụng Bất đẳng thức Cauchy Schwarz

Việc giải các bài tập Bất đẳng thức Cauchy Schwarz đòi hỏi nắm vững các kỹ thuật áp dụng và biến đổi phù hợp. Phương pháp cơ bản là chuyển về dạng tổng các bình phương và tích các số hạng.

Một trong những kỹ thuật quan trọng là nhận diện được dạng bất đẳng thức cần chứng minh có thể áp dụng Cauchy Schwarz. Thông thường, các biểu thức chứa tổng tích của hai dãy số hoặc hai hàm số sẽ gợi ý việc sử dụng bất đẳng thức này.

Sau khi xác định được khả năng áp dụng, việc biến đổi về dạng chuẩn của bất đẳng thức là bước then chốt. Điều này thường đòi hỏi các kỹ năng tính toán đại số và phân tích biểu thức một cách linh hoạt.

Các dạng bài tập điển hình

Bất đẳng thức Cauchy Schwarz trong giải tích thường xuất hiện dưới nhiều dạng khác nhau. Dạng phổ biến nhất là chứng minh bất đẳng thức liên quan đến tích phân của hai hàm số trên một khoảng.

Trong đại số, các bài toán thường yêu cầu chứng minh bất đẳng thức liên quan đến tổng của các số thực. Đặc biệt là các bài toán về cực trị, tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức.

Ngoài ra còn có các dạng bài tập ứng dụng trong hình học, đặc biệt là các bài toán về khoảng cách và góc giữa các vector trong không gian.

Hướng dẫn giải chi tiết kèm ví dụ

Để giải thành công các bài tập về bất đẳng thức Cauchy Schwarz, cần tuân theo quy trình giải có hệ thống. Bước đầu tiên là phân tích kỹ đề bài để xác định dạng bài tập và phương pháp tiếp cận phù hợp.

Tiếp theo là việc biến đổi biểu thức về dạng chuẩn của bất đẳng thức. Quá trình này có thể đòi hỏi nhiều bước trung gian và kỹ năng tính toán chính xác.

Cuối cùng là kiểm tra lại kết quả và xem xét các trường hợp đặc biệt khi dấu đẳng thức xảy ra. Việc này giúp hoàn thiện lời giải và đảm bảo tính chặt chẽ của chứng minh.

Bài tập về đại số

Trong lĩnh vực đại số, giải Bất đẳng thức Cauchy Schwarz thường bắt đầu bằng việc xác định hai dãy số cần áp dụng bất đẳng thức. Điều này đòi hỏi khả năng nhìn nhận và phân tích biểu thức một cách sáng tạo.

Việc biến đổi về dạng chuẩn trong đại số thường đơn giản hơn so với giải tích. Tuy nhiên, khó khăn nằm ở việc lựa chọn cách biến đổi tối ưu và hiệu quả nhất.

Sau khi áp dụng bất đẳng thức, việc rút gọn và sắp xếp các số hạng cần được thực hiện cẩn thận để đi đến kết luận cuối cùng một cách chính xác.

Bài tập về giải tích

Trong giải tích, các b

Bất đẳng thức Cauchy Schwarz là một trong những công cụ quan trọng trong toán học, giúp rút ra nhiều hệ quả quý giá trong giải tích và hình học. Việc nắm vững bất đẳng thức Cauchy Schwarz không chỉ hỗ trợ giải bài tập hiệu quả mà còn mở ra nhiều hướng đi mới trong nghiên cứu và ứng dụng. Các phương pháp chứng minh đa dạng và ứng dụng phong phú giúp học sinh phát triển tư duy logic, làm nền tảng vững chắc cho các kiến thức nâng cao hơn.