Cách lập bảng biến thiên chi tiết và hướng dẫn thực hành hiệu quả

Cách lập bảng biến thiên là một kỹ năng quan trọng trong toán học. Để hiểu rõ hơn, hãy khám phá các bước và phương pháp lập bảng biến thiên cho các hàm số khác nhau. Bài viết này sẽ hướng dẫn bạn chi tiết cách vẽ bảng biến thiên, từ lý thuyết đến thực hành.

Cách lập bảng biến thiên và các bước thực hiện cơ bản

Bảng biến thiên là gì – một công cụ toán học quan trọng giúp khảo sát sự thay đổi của hàm số thông qua việc biểu diễn các thông tin về dấu, giá trị và xu hướng tăng/giảm của hàm số tại các khoảng xác định. Bảng biến thiên giúp người học hình dung rõ ràng hơn về quy luật biến đổi của hàm số.

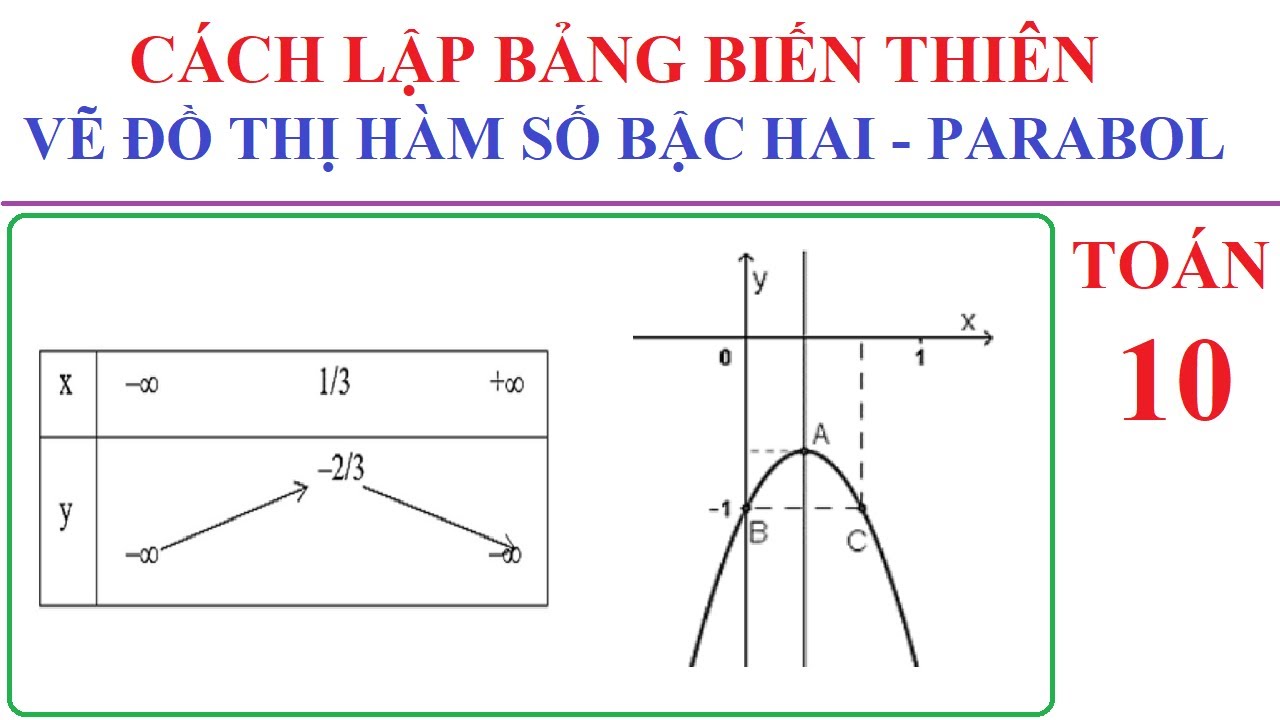
Để cách lập bảng biến thiên được chính xác và đầy đủ, cần thực hiện theo trình tự: Xác định miền xác định của hàm số, tìm các điểm làm hàm số đạt cực trị hoặc không xác định, chia miền xác định thành các khoảng, khảo sát dấu đạo hàm trên từng khoảng để xác định xu hướng biến thiên.

Khi lập bảng, cần tuân thủ nguyên tắc: Vẽ khung bảng với các hàng thể hiện x, f'(x), f(x); Điền các giá trị x đặc biệt vào cột tương ứng theo thứ tự từ trái sang phải; Xác định dấu đạo hàm và xu hướng biến thiên trên từng khoảng; Tính giá trị hàm số tại các điểm đặc biệt và điền vào bảng.

Việc thực hành nhiều bài tập đa dạng sẽ giúp nâng cao kỹ năng lập và sử dụng bảng biến thiên hiệu quả. Đây là công cụ không thể thiếu khi giải các bài toán về cực trị, giá trị lớn nhất, nhỏ nhất của hàm số.

Phương pháp xác định điểm đặc biệt và khoảng xét dấu khi lập bảng biến thiên

Phương pháp lập bảng biến thiên cần tuân theo các bước có tính hệ thống để xác định chính xác điểm đặc biệt và khoảng xét dấu. Việc xác định điểm đặc biệt đóng vai trò then chốt, giúp phân chia các khoảng xét dấu một cách hợp lý và chính xác.

Khi xác định điểm đặc biệt, cần tìm các điểm mà tại đó hàm số không xác định hoặc không liên tục. Điều này bao gồm việc tìm nghiệm của mẫu số, điểm gián đoạn và các điểm mà đạo hàm bằng 0 hoặc không tồn tại. Tương tự như cách xác định biến cố độc lập trong xác suất thống kê, mỗi điểm đặc biệt cần được xem xét độc lập với các điểm khác.

Sau khi có các điểm đặc biệt, việc chia khoảng xét dấu được thực hiện bằng cách sắp xếp các điểm theo thứ tự tăng dần trên trục số. Các khoảng này sẽ được phân tích riêng biệt để xác định dấu của đạo hàm, từ đó xác định được tính đơn điệu của hàm số trên từng khoảng. Việc phân tích kỹ lưỡng từng khoảng giúp đảm bảo tính chính xác của bảng biến thiên cuối cùng.

Hướng dẫn chi tiết cách vẽ bảng biến thiên cho các dạng hàm số phổ biến

Bảng biến thiên là công cụ quan trọng giúp phân tích sự biến đổi của hàm số. Cách lập bảng biến thiên chuẩn xác sẽ giúp xác định được các đặc trưng của hàm số như tính đơn điệu, cực trị, giá trị lớn nhất, nhỏ nhất. Việc nắm vững cách vẽ bảng biến thiên cho từng dạng hàm số sẽ giúp giải quyết nhiều bài toán phức tạp.

Cách vẽ bảng biến thiên cho hàm bậc nhất

Với hàm bậc nhất y = ax + b (a ≠ 0), ta xác định dấu của hệ số a để biết chiều biến thiên của hàm số. Khi a > 0, hàm số đồng biến trên toàn tập xác định. Ngược lại khi a < 0, hàm số nghịch biến trên toàn tập xác định. Ví dụ với hàm số y = 2x + 1, do a = 2 > 0 nên hàm số đồng biến trên R. Giá trị của hàm số tăng dần từ -∞ đến +∞ khi x tăng từ -∞ đến +∞. Điều này được thể hiện rõ qua mũi tên hướng lên trong bảng biến thiên.

Phương pháp lập bảng biến thiên hàm bậc hai

Với hàm bậc hai y = ax² + bx + c (a ≠ 0), ta cần xác định đỉnh của parabol thông qua công thức x = -b/2a. Đỉnh này chính là điểm cực trị của hàm số.

Khi a > 0, parabol có dạng cong lên và điểm cực trị là cực tiểu. Hàm số giảm trên (-∞; -b/2a) và tăng trên (-b/2a; +∞). Ngược lại khi a < 0, parabol có dạng cong xuống và điểm cực trị là cực đại. Vẽ bảng biến thiên cần thể hiện rõ sự thay đổi này.

Bảng biến thiên cho hàm phân thức

Với hàm phân thức y = P(x)/Q(x), ta cần xác định tập xác định bằng cách giải Q(x) ≠ 0. Sau đó tìm các điểm mà đạo hàm bằng 0 hoặc không xác định để chia tập xác định thành các khoảng đơn điệu.

Xét dấu của đạo hàm trên từng khoảng để xác định chiều biến thiên. Đặc biệt cần chú ý các điểm gián đoạn và cách tiếp cận của hàm số tại các điểm này. Việc vẽ các mũi tên thể hiện sự tiến đến +∞ hay -∞ cần được thực hiện cẩn thận và chính xác.

Các ví dụ minh họa về lập bảng biến thiên hàm số bậc 2 và phân tích chi tiết

Việc lập bảng biến thiên hàm bậc 2 đóng vai trò quan trọng trong việc phân tích đặc điểm và tính chất của hàm số. Thông qua các ví dụ cụ thể, chúng ta sẽ thấy được cách xây dựng và phân tích bảng biến thiên hàm số bậc 2 một cách chi tiết và hiệu quả.

Ví dụ 1: Hàm số bậc 2 dạng cơ bản

Xét hàm số y = x² – 2x – 3. Để lập bảng biến thiên, trước tiên cần tìm đạo hàm y’ = 2x – 2. Điểm cực trị x₀ = 1 là nghiệm của phương trình y’ = 0. Giá trị của hàm số tại x₀ là y(1) = -4.

Khi x < 1, đạo hàm âm nên hàm số giảm. Khi x > 1, đạo hàm dương nên hàm số tăng. Điểm (1; -4) là điểm cực tiểu của hàm số. Đồ thị hàm số là parabol mở lên, cắt trục hoành tại x = -1 và x = 3.

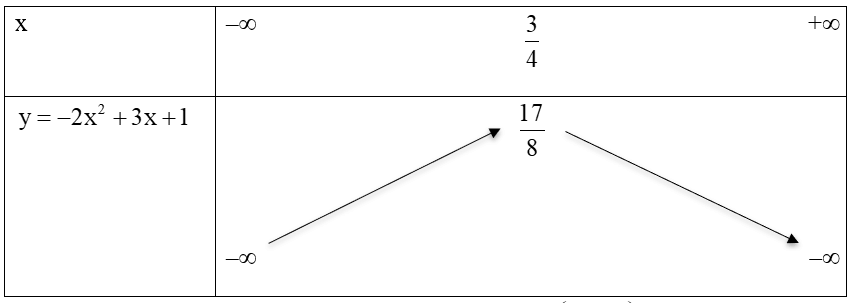
Ví dụ 2: Hàm số bậc 2 có điểm đặc biệt

Xét hàm số y = -2x² + 4x + 1. Đạo hàm y’ = -4x + 4 cho điểm cực trị x₀ = 1. Tại x₀, giá trị cực đại của hàm số là y(1) = 3. Hệ số a = -2 < 0 nên đồ thị là parabol mở xuống.

Khi x < 1, đạo hàm dương nên hàm số tăng. Khi x > 1, đạo hàm âm nên hàm số giảm. Điểm (1; 3) là điểm cực đại của hàm số. Đồ thị cắt trục hoành tại hai điểm có hoành độ x₁ ≈ -0.37 và x₂ ≈ 2.37.

Ví dụ 3: Bài toán thực tiễn

Một công ty sản xuất đồ chơi nghiên cứu mối quan hệ giữa giá bán (x triệu đồng) và lợi nhuận (y triệu đồng) theo công thức y = -x² + 10x – 16. Việc lập bảng biến thiên hàm số bậc 2 giúp xác định mức giá tối ưu.

Qua phân tích đạo hàm y’ = -2x + 10, tìm được điểm cực đại x₀ = 5. Tại x₀, lợi nhuận đạt cực đại y(5) = 9 triệu đồng. Khi x < 5, lợi nhuận tăng theo giá bán. Khi x > 5, lợi nhuận giảm khi tăng giá. Do đó, công ty nên định giá sản phẩm ở mức 5 triệu đồng để tối đa hóa lợi nhuận.

Những lưu ý quan trọng khi lập bảng biến thiên đầy đủ và chính xác

Việc lập bảng biến thiên đầy đủ đòi hỏi sự tỉ mỉ và chính xác trong từng bước. Điểm mấu chốt là phải xác định đúng các điểm đặc biệt của hàm số như điểm cực trị, điểm uốn, điểm gián đoạn và các điểm mà đạo hàm bằng 0 hoặc không tồn tại.

Khi phân tích dấu của đạo hàm, cần chia miền xét thành các khoảng con và xét kỹ sự biến thiên trên từng khoảng. Đặc biệt chú ý các điểm gián đoạn để tránh bỏ sót thông tin quan trọng về tính liên tục của hàm số.

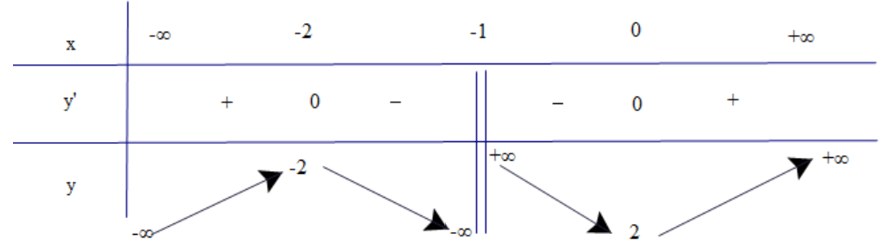
Một yếu tố then chốt khác là việc kiểm tra tính hợp lý của kết quả bằng cách vẽ đồ thị sơ bộ hoặc tính giá trị hàm số tại một số điểm đặc trưng. Điều này giúp phát hiện sai sót trong quá trình lập bảng.

Các sai lầm thường gặp

Một trong những lỗi phổ biến nhất khi lập bảng biến thiên thực tiễn là bỏ sót các điểm đặc biệt của hàm số. Theo thống kê của Trung tâm Toán học GeoGebra, khoảng 40% học sinh mắc lỗi này trong các bài kiểm tra.

Việc nhầm lẫn dấu của đạo hàm trên các khoảng cũng là sai sót thường xuyên xảy ra. Nguyên nhân chủ yếu do không kiểm tra kỹ các điểm biên của khoảng xét và vội vàng kết luận về chiều biến thiên.

Ngoài ra, nhiều người còn mắc lỗi khi xác định giá trị của hàm số tại các điểm gián đoạn, dẫn đến việc vẽ sai hướng mũi tên biểu diễn sự biến thiên.

Mẹo kiểm tra kết quả

Phương pháp hiệu quả để kiểm tra độ chính xác của bảng biến thiên là vẽ đồ thị sơ bộ dựa trên các thông tin đã có. Nếu đồ thị không mâu thuẫn với các kết luận trong bảng, khả năng cao bảng biến thiên đã được lập đúng.

Một cách khác là tính giá trị của hàm số tại các điểm đặc biệt và một số điểm trung gian để xác nhận chiều biến thiên đã xác định. Việc này giúp phát hiện các sai sót về dấu của đạo hàm.

Kiểm tra tính liên tục của hàm số tại các điểm đặc biệt cũng rất quan trọng. Nếu hàm số gián đoạn, cần đảm bảo các mũi tên trong bảng biến thiên phản ánh đúng tính chất này.

Ứng dụng thực tiễn của bảng biến thiên

Bảng biến thiên hàm số được ứng dụng rộng rãi trong nhiều lĩnh vực thực tế. Trong kinh tế, các chuyên gia sử dụng bảng biến thiên để phân tích xu hướng biến động giá cả, doanh thu và lợi nhuận theo thời gian.

Trong lĩnh vực kỹ thuật, kỹ sư sử dụng bảng biến thiên để nghiên cứu sự thay đổi của các thông số như nhiệt độ, áp suất, vận tốc trong quá trình vận hành máy móc.

Hướng dẫn thực hành và bài tập rèn luyện về lập bảng biến thiên

Việc nắm vững cách lập bảng biến thiên là kỹ năng quan trọng giúp học sinh phân tích được sự biến đổi của hàm số. Để thành thạo kỹ năng này, cần thực hành qua nhiều dạng bài tập khác nhau với độ khó tăng dần.

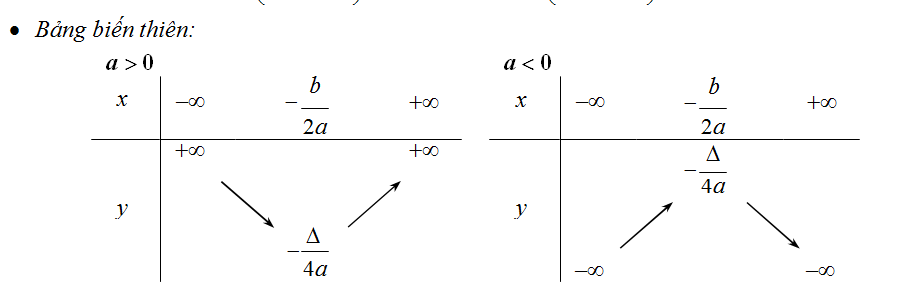
Hướng dẫn lập bảng biến thiên cần tuân theo các bước cơ bản: xác định tập xác định, tìm các điểm đặc biệt, tính giá trị hàm số tại các điểm đặc biệt và xét dấu đạo hàm để xác định chiều biến thiên. Việc thực hành nhiều sẽ giúp rèn luyện tư duy logic và khả năng phân tích.

Sau đây là một số bài tập mẫu và bài tập tự luyện để giúp củng cố kiến thức về lập bảng biến thiên.

Bài tập mẫu có lời giải

Bài 1: Lập bảng biến thiên của hàm số y = x³ – 3x trên R

• Bước 1: Tập xác định là R
• Bước 2: y’ = 3x² – 3 = 3(x² – 1) = 3(x+1)(x-1)
• Bước 3: Điểm đặc biệt x = -1 và x = 1
• Bước 4: Lập bảng biến thiên và kết luận

Bài 2: Lập bảng biến thiên của hàm số y = x⁴ – 2x²
Đây là một hàm số chẵn nên ta chỉ cần xét nửa bảng biến thiên rồi lấy đối xứng qua trục tung.

Bài tập tự luyện

Để nâng cao kỹ năng lập bảng biến thiên, học sinh có thể thực hành với các bài tập sau:

• Lập bảng biến thiên của hàm số y = x³ + 3x² trên R
• Khảo sát sự biến thiên của hàm số y = (x² + 1)/(x – 2)
• Xét tính đơn điệu của hàm số y = x⁴ – 4x³ + 4x

Việc giải các bài tập này giúp rèn luyện khả năng tính toán và phân tích một cách có hệ thống. Mỗi bài tập đều có những đặc điểm riêng, đòi hỏi sự linh hoạt trong cách tiếp cận và xử lý.

Tóm lại, cách lập bảng biến thiên là một kỹ năng quan trọng giúp bạn phân tích đặc điểm của hàm số một cách rõ ràng. Việc nắm vững các bước xác định điểm đặc biệt và cách vẽ bảng biến thiên cho từng dạng hàm sẽ giúp ích rất nhiều trong quá trình giải toán. Thông qua các ví dụ thực tiễn và bài tập, bạn sẽ tự tin và chính xác hơn trong các phép tính của mình.