Chứng minh hình bình hành là dạng bài toán khá thú vị, thường xuất hiện trong các bài kiểm tra quan trọng. Ngoài ra, chúng còn được ứng dụng phổ biến trong thực tiễn cuộc sống, phục vụ con người trong nhiều nghiên cứu, phát minh ở các lĩnh vực khoa học khác nhau. Hãy cùng chúng tôi trau dồi kiến thức về dạng toán này tại bài viết dưới đây.
Định nghĩa hình bình hành
Hình bình hành là tứ giác có các cặp cạnh đối song song với nhau.
Có thể bạn quan tâm: Tìm hiểu về hình bình hành là gì? Các đặc điểm nổi bật của dạng hình này
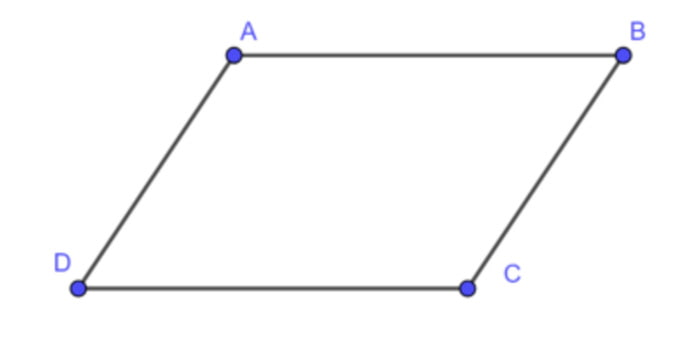
Ví dụ minh họa: Cho hình bình hành ABCD,
Từ nội dung định nghĩa trên ta có:
- AB//CD
- AD//BC
Tính chất hình bình hành:
- Hình bình hành có các cạnh đối song song và bằng nhau.
- Hình bình có các góc đối bằng nhau.
- Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường.
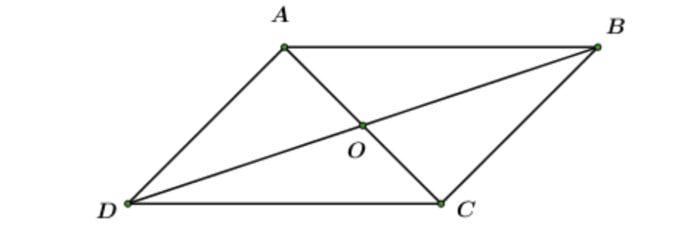
Hình bình hành ABCD, gọi O là giao điểm của 2 đường chéo AC và BD.
Từ đây ta có:
- AB = CD
- AD = BC
- A = C và B = D
- OA = OC và OD = OB
Các bạn cần tìm hiểu và ghi nhớ một cách chuẩn xác những kiến thức trên, tránh nhầm lẫn với nhiều khái niệm khác trong toán học.
Bạn cần biết: Cách dấu hiệu nhận biết hình bình hành chuẩn xác
Cách chứng minh hình bình hành
Để chứng minh hình bình hành, các bạn có thể dựa vào định nghĩa, các tính chất của hình bình hành để xác định phương hướng chứng minh. Dưới đây là một số dạng toán quan trọng:
Chứng minh tứ giác có 2 cặp cạnh đối song song
Trường hợp này, thật đơn giản khi bạn có thể dựa vào nội dung định nghĩa về hình bình hành để suy ra kết luật.
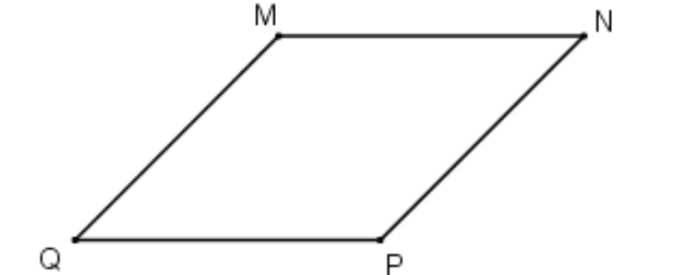
Ví dụ minh họa: Tứ giác MNPQ có MN//PQ và MQ//NP ⇒ MNPQ là hình bình hành (dựa theo định nghĩa về hình bình hành)
Chứng minh tứ giác có các cặp cạnh đối bằng nhau
Khi đề bài cho một tứ giác có các cặp cạnh đối bằng nhau, các bạn sẽ phát triển bài toán để xác định các cặp cạnh đó cũng song song với nhau, suy ra tứ giác là hình bình hành.
Ví dụ minh họa: Cho tứ giác MNPQ có MN = PQ và MQ = NP. Chứng minh MNPQ là hình bình hành.
Chứng minh:
Xét ∆MNP và ∆PQM ta có:
- Cạnh MP chung
- MN = PQ (gt)
- MQ = NP (gt)
⇒ ∆MNP = ∆PQM (c.c.c)
⇒ ∠PMQ = ∠MPN nên NP//PQ (2 góc so le bằng nhau) (1)
Và ∠MQP = ∠MNP nên MQ//NP (2 góc so le bằng nhau) (2)
Kết hợp (1) và (2) suy ra MNPQ là hình bình hành
Chứng minh tứ giác có 1 cặp cạnh đối song song và bằng nhau
Từ định nghĩa, tính chất của hình bình hành, ta được:
MN // PQ
MN = PQ
MI = IN
QK = KP
MI // KP và MI = KP
Chứng minh tứ giác có 2 cặp góc đối bằng nhau
Dựa vào dữ kiện bài toán, các em phát triển theo hướng chứng minh 2 tam giác gắn với các góc đối bằng nhau.
Ví dụ minh họa: Cho tứ giác MNPQ, có ∆MNQ = ∆NPQ và ∆MNP = ∆MQP.
Có ∆MNQ = ∆NPQ ⇒ NMQ = NPQ (1)
∆MNP = ∆MQP ⇒ MNP = MQP (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình bình hành (2 góc đối bằng nhau)
Chứng minh tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường
Dựa vào dữ kiện bài toán, các bạn chứng minh tứ giác đã cho có một cặp cạnh đối song song và bằng nhau.
Ví dụ minh họa: Cho tứ giác MNPQ, MP cắt NQ tại I và I là trung điểm của MP và NQ.
Xét ∆NIP và ∆QIM ta có:
- IN = IQ (gt)
- IM = IP (gt)
- NIP=QIM (2 góc đối đỉnh)
⇒ ∆NIP = ∆QIM (c.g.c)
⇒ MQ = NP (1)
Và ∠INP = ∠IQM (2 góc so le) suy ra MQ//NP (2)
Từ (1) và (2) chứng minh được tứ giác MNPQ là hình bình hành
Tìm hiểu thêm: Các tính chất đường chéo hình bình hành quan trọng
Ứng dụng của việc chứng minh hình bình hành trong thực tế
Chứng minh một tứ giác là hình bình hành đã được ứng dụng phổ biến trong rất nhiều lĩnh vực như kiến trúc, sản xuất, kỹ thuật bản đồ hay giáo dục đều sử dụng nó để tìm kiếm phương án thi công tối ưu nhất. Cụ thể như sau:
- Lĩnh vực thiết kế kiến trúc: Các kỹ sư sử dụng các tính chất, định nghĩa của hình bình hành để tìm kiếm sự hài hòa, đối xứng trong thiết kế.
- Lĩnh vực công nghiệp sản xuất: Trong các nhà máy, việc sắp xếp máy móc và lắp đặt các bộ phận yêu cầu độ chuẩn xác cao. Chứng minh các yếu tố này tạo nên hình bình hành giúp kỹ sư tối ưu hóa không gian và nâng cao hiệu quả sản xuất.
- Lĩnh vực giáo dục và nghiên cứu: Ở đây đã quá rõ ràng, các em học sinh và thầy cô giáo sử dụng cách chứng minh hình bình hành để giải quyết các bài toán hình học phức tạp, từ đây hướng đến nội dung kiến thức sâu hơn.

Nội dung đã khẳng định những giá trị tích cực của kiến thức không chỉ nằm trong phạm vi học thuật mà còn được ứng dụng rộng rãi trong các lĩnh vực quan trọng khác của cuộc sống.
Có thể bạn quan tâm: Giải thích “Hình bình hành có tâm đối xứng không?” chi tiết
Một số bài tập thực hành tại nhà
Để ghi nhớ và phát triển kỹ năng giải toán chứng minh hình bình hành, các bạn phải tích cực giải các dạng đề liên quan. Dưới đây là một số bài tập thực hành tại nhà:
Bài tập 1: Cho hình bình hành MNPQ, đường chéo NQ. Kẻ MH và PK vuông góc với NQ lần lượt tại H và tại K. Chứng minh tứ giác MHPK là hình bình hành.
Bài tập 2: Tứ giác MNPQ. Gọi E, F, G, H theo thứ tự là trung điểm của NQ, MN, MP, PQ.
- Chứng minh: EFGH là hình bình hành
- Cho MQ = a, NP = b. Tính chu vi hình hình hành EFGH.
Bài tập 3: Cho tam giác MNH, trực tâm H. Các đường thẳng vuông góc với MN tại N, vuông góc với MC tại C cắt nhau tại D. Chứng minh:
- NDCH là hình bình hành
- NMC + NDC = 180°
- H, I, D thẳng hàng (I là trung điểm NC)
Hy vọng những chia sẻ trên đây của chúng tôi sẽ giúp bạn biết cách chứng minh hình bình hành một cách ngắn gọn và chuẩn xác. Đừng quên theo dõi bài viết khác của chúng tôi để cập nhật nhiều kiến thức bổ ích!




