Công thức hạ bậc lượng giác là một công cụ hữu ích trong toán học, đặc biệt là trong lĩnh vực lượng giác, giúp đơn giản hóa các biểu thức lượng giác chứa các hàm lượng giác có bậc cao hơn. Việc sử dụng công thức hạ bậc giúp cho việc giải toán, chứng minh định lý và ứng dụng lượng giác trở nên dễ dàng và hiệu quả hơn. Cùng chúng tôi thông qua bài viết dưới đây tìm hiểu rõ hơn về nội dung này nhé.
Công thức hạ bậc là gì?
Công thức hạ bậc lượng giác là một tập hợp các phương trình cho phép chuyển đổi các hàm lượng giác bậc cao (như sin²x, cos²x, tan²x) thành các biểu thức tương đương chứa các hàm lượng giác của góc đơn hoặc góc kép.

Cụ thể, những ct hạ bậc này giúp biểu diễn bình phương (hoặc lũy thừa cao hơn) của các hàm sin, cos, tan thành tổng hoặc hiệu của các hàm lượng giác cơ bản. Ví dụ, sin²x có thể được biểu diễn thành (1 – cos2x)/2.
Công thức lượng giác hạ bậc đóng vai trò quan trọng trong việc đơn giản hóa các biểu thức lượng giác phức tạp, giải quyết các phương trình và bất phương trình lượng giác, cũng như trong tích phân các hàm lượng giác. Việc sử dụng thành thạo các công thức này không chỉ giúp tối ưu hóa quá trình tính toán mà còn mở ra nhiều phương pháp giải quyết sáng tạo cho các bài toán lượng giác nâng cao.
Các công thức hạ bậc lượng giác phổ biến
Dưới đây là những ct hạ bậc được sử dụng phổ biến trong lượng giác học hiện nay như: công thức hạ bậc cos, sin…
Công thức hạ bậc bậc 2
Đây là những công thức cơ bản nhất và được sử dụng phổ biến nhất. Chúng là những công thức hạ bậc cos, sin nguyên bản giúp chuyển đổi bình phương của hàm sin, cos và tan thành biểu thức chứa hàm góc đơn hoặc góc kép:
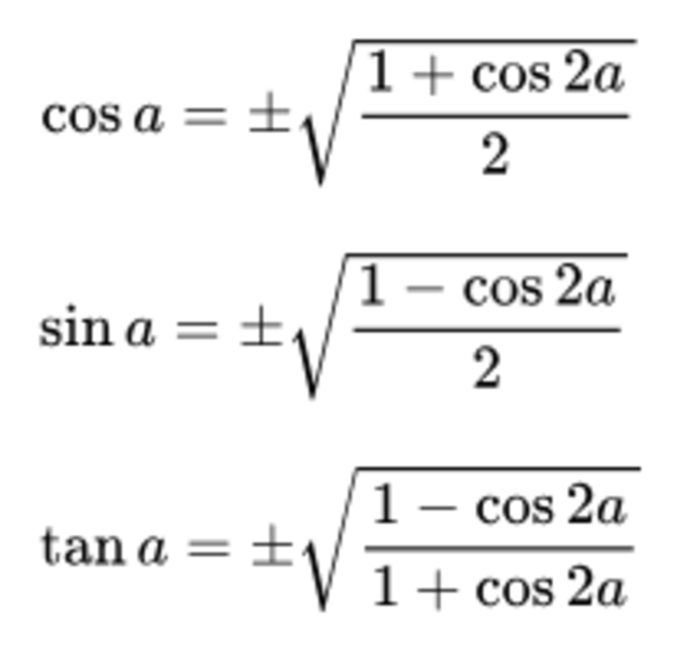
Công thức lùi bậc bậc 3
Các công thức hạ bậc 3 giúp biểu diễn lũy thừa bậc ba của sin và cos thành tổ hợp của hàm góc đơn và góc ba. Chúng đặc biệt hữu ích trong việc tính tích phân của các hàm lượng giác bậc cao:
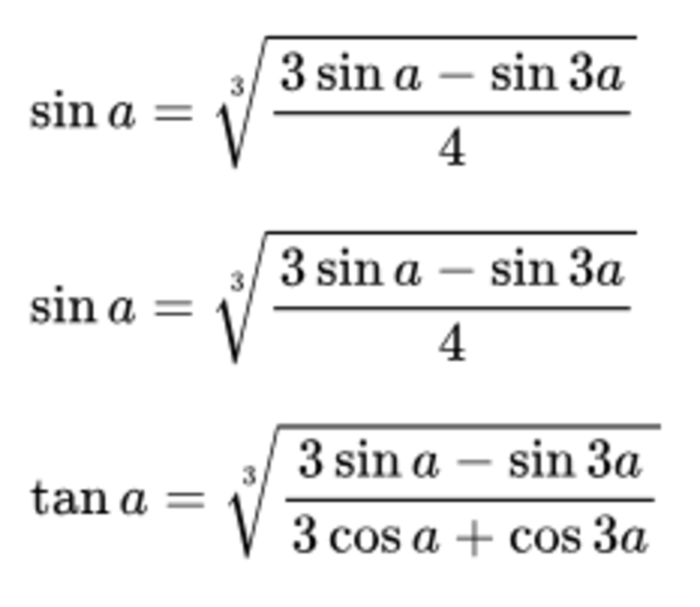
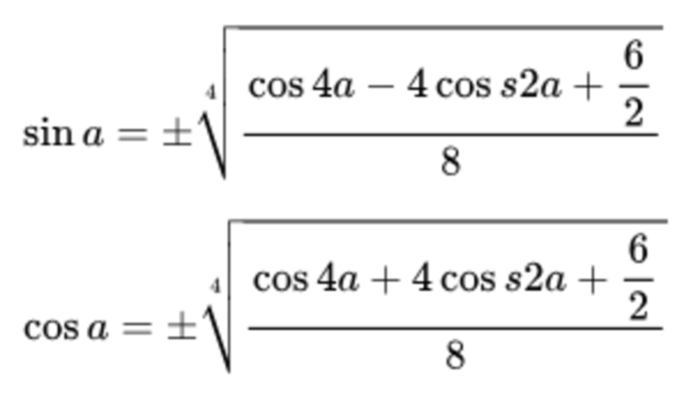
Công thức giảm bậc bậc 4
Công thức hạ bậc 4 cho phép chúng ta biểu diễn lũy thừa bậc bốn của sin và cos thành tổ hợp của hàm góc kép và góc bốn. Những công thức này thường được sử dụng trong các bài toán phức tạp hơn và trong lý thuyết dao động:
Công thức giảm bậc bậc 5
Đây là những công thức hạ bậc sin cos mở bậc 5 phức tạp hơn, biểu diễn lũy thừa bậc năm của sin và cos thành tổ hợp của hàm góc đơn, góc ba và góc năm. Mặc dù ít được sử dụng hơn, chúng vẫn có ứng dụng quan trọng trong một số lĩnh vực chuyên sâu của toán học và vật lý:

Các công thức lùi bậc khác
Bên cạnh các công thức hạ bậc phổ thông trên, bạn có thể tham khảo các công thức khác như:
Cách giảm bậc sin mũ 2, cos mũ 2, tan mũ 2
Dưới đây là các cách hạ bậc sin mũ 2, cos mũ 2, tan mũ 2 nâng cao hơn nhưng không kém phần quan trọng.
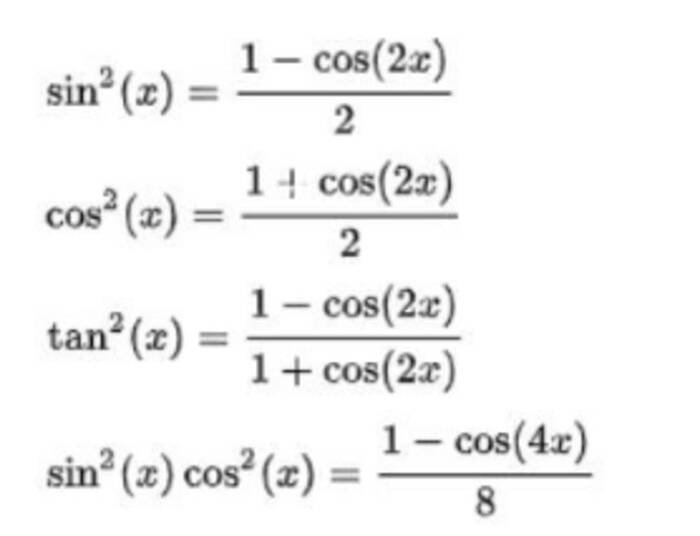
Hạ bậc cos mũ 2, sin mũ 2.. là những phương pháp hiệu quả trong việc đơn giản hóa những bài toán phức tạp.
Công thức giảm bậc sin, cos mũ 3
CT hạ bậc cos mũ 3, sin mũ 3 là những công cụ quan trọng trong lượng giác học nâng cao. Chúng cho phép chúng ta biểu diễn lũy thừa bậc ba của hàm sin và cos thành tổ hợp tuyến tính của các hàm lượng giác của góc đơn và góc ba lần.
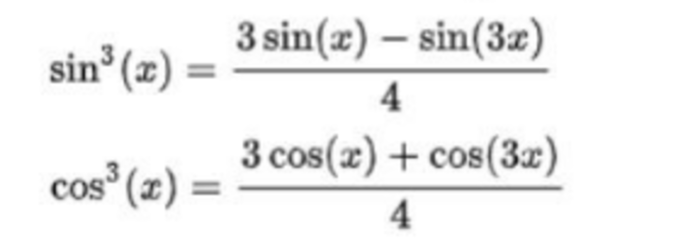
Công thức thoái bậc sin, cos mũ 4
Công thức hạ bậc cos mũ 4, sin mũ 4 là những công cụ mạnh mẽ trong lượng giác học, đặc biệt hữu ích khi đối mặt với các biểu thức lượng giác phức tạp bậc cao. Những công thức này cho phép chúng ta biểu diễn lũy thừa bậc bốn của hàm sin và cos thành tổ hợp của các hàm lượng giác của góc đơn, góc kép và góc bốn lần.

Các trường hợp hạ bậc đặc biệt
Công thức hạ bậc cos2x là một trong những công thức quan trọng trong lượng giác học, cho phép chúng ta biểu diễn cosin của góc kép thông qua các hàm lượng giác của góc đơn.
Công thức này có nhiều ứng dụng trong việc đơn giản hóa biểu thức lượng giác, giải phương trình, và tính toán trong nhiều lĩnh vực như vật lý và kỹ thuật. Đặc biệt, nó tạo ra mối liên hệ giữa các hàm lượng giác của góc kép và góc đơn thông qua chứng minh công thức hạ bậc lượng giác. Điều này giúp chúng ta chuyển đổi giữa các dạng biểu thức khác nhau.
Dưới đây là công thức cos 2x hạ bậc: cos 2x = cos²x – sin²x = 2cos²x – 1 = 1 – 2sin²x
Lời kết
Có thể tháy, công thức hạ bậc đóng vai trò then chốt trong lượng giác học, cung cấp những công cụ mạnh mẽ để đơn giản hóa và giải quyết các biểu thức lượng giác phức tạp. Từ công thức cơ bản cho sin²x và cos²x đến những công thức phức tạp hơn cho các lũy thừa bậc cao, mỗi công thức đều có vai trò riêng trong việc mở rộng khả năng tính toán và phân tích của chúng ta.