Hướng dẫn chi tiết cách tính diện tích hình thoi từ công thức đến bài tập thực tế

Diện tích hình thoi là một khái niệm quan trọng trong hình học phẳng. Để nắm vững cách tính diện tích hình thoi, bạn cần hiểu rõ các công thức và quy tắc liên quan. Bài viết này sẽ hướng dẫn cụ thể từng phương pháp tính toán và áp dụng trong thực tiễn.

Diện tích hình thoi và các khái niệm cơ bản trong hình học phẳng

Trước khi tìm hiểu về diện tích hình thoi, cần nắm rõ hình thoi là gì. Đây là một khái niệm quan trọng giúp việc tính toán diện tích trở nên dễ dàng và chính xác hơn.

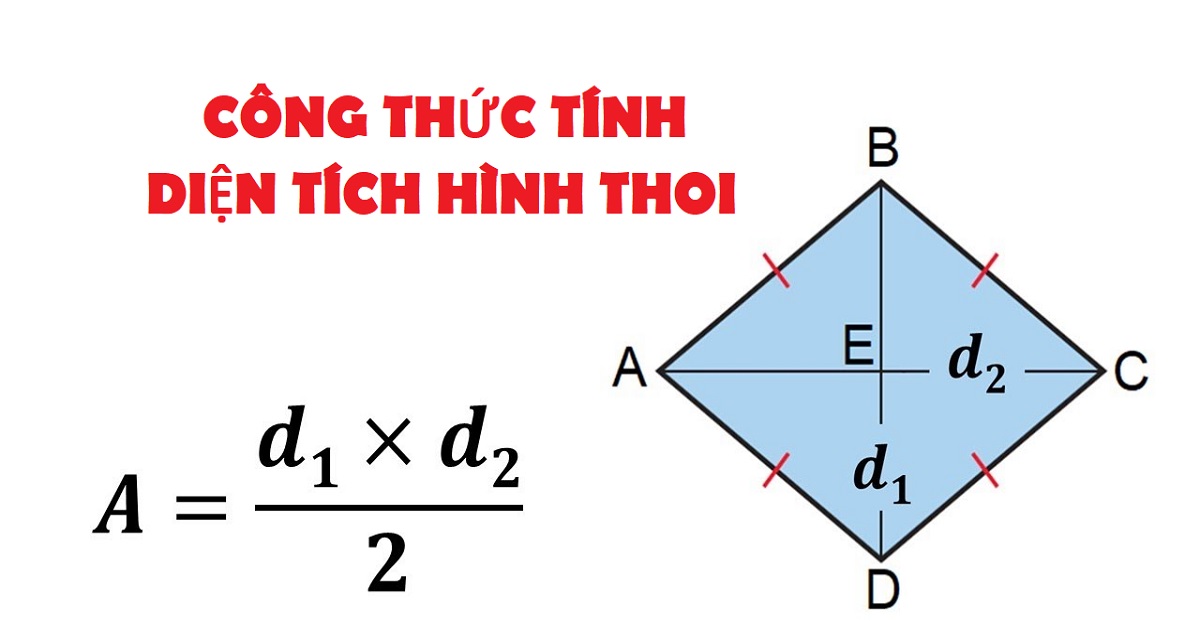
Diện tích hình thoi được xác định bằng tích của hai đường chéo chia đôi nhau. Công thức tính diện tích hình thoi là S = (d1 x d2)/2, trong đó d1 và d2 lần lượt là độ dài hai đường chéo của hình thoi. Công thức này được áp dụng phổ biến trong các bài toán hình học phẳng.

Ngoài ra, diện tích hình thoi còn có thể được tính bằng tích của cạnh và đường cao. Với a là độ dài cạnh và h là đường cao, diện tích hình thoi được tính theo công thức S = a x h. Cách tính này đặc biệt hữu ích khi không biết độ dài các đường chéo nhưng lại có thông tin về cạnh và đường cao.

Việc nắm vững các công thức tính diện tích này giúp giải quyết nhiều bài toán thực tế, từ tính diện tích mặt sàn hình thoi đến thiết kế các công trình kiến trúc có hình dạng đặc biệt này. Đồng thời, kiến thức về hình thoi cũng là nền tảng quan trọng để học tập các khái niệm phức tạp hơn trong hình học không gian.

Công thức tính diện tích hình thoi và các phương pháp áp dụng trong thực tế

Công thức tính diện tích hình thoi là một trong những kiến thức toán học cơ bản được ứng dụng rộng rãi trong thực tế. Việc tính diện tích hình thoi có thể thực hiện theo nhiều cách khác nhau tùy thuộc vào các yếu tố đã biết.

Trong kiến trúc và thiết kế, các kiến trúc sư thường sử dụng hình thoi để tạo nên những mẫu gạch lát sàn độc đáo hoặc thiết kế các ô cửa sổ mang tính thẩm mỹ cao. Việc nắm vững cách tính diện tích hình thoi giúp họ tính toán chính xác số lượng vật liệu cần thiết.

Công thức tính diện tích hình thoi dựa trên đường chéo

Diện tích hình thoi được tính bằng tích của hai đường chéo chia cho 2. Đây là phương pháp đơn giản và phổ biến nhất. cách tính đường chéo hình thoi sẽ giúp bạn xác định chính xác độ dài đường chéo khi cần thiết.

Công thức này đặc biệt hữu ích trong ngành thiết kế thời trang, khi các nhà thiết kế cần tính toán lượng vải cần thiết cho các họa tiết hình thoi trên trang phục. Nhiều thương hiệu nổi tiếng như Burberry thường sử dụng mẫu hình thoi trong các thiết kế đặc trưng của họ.

Công thức tính diện tích hình thoi dựa trên cạnh và góc

Phương pháp này sử dụng độ dài cạnh và góc của hình thoi để tính diện tích. Công thức này thường được áp dụng khi không thể đo trực tiếp được đường chéo của hình thoi.

Trong công nghiệp sản xuất, nhiều nhà máy sử dụng công thức này để tính toán diện tích các tấm kim loại hình thoi cần cắt. Điều này giúp tối ưu hóa việc sử dụng nguyên liệu và giảm thiểu lãng phí.

Trường hợp biết độ dài cạnh và sin của góc

Khi biết độ dài cạnh a và sin của góc α, diện tích hình thoi được tính theo công thức S = a² × sin α. Công thức này thường được sử dụng trong các bài toán hình học phức tạp.

Trong lĩnh vực xây dựng, các kỹ sư thường áp dụng công thức này khi thiết kế các kết cấu mái nhà có dạng hình thoi. Ví dụ, công trình Nhà hát Opera Sydney nổi tiếng có nhiều phần mái được thiết kế dựa trên nguyên lý này.

Trường hợp biết độ dài cạnh và độ của góc

Khi góc được cho dưới dạng độ, ta cần chuyển đổi sang radian trước khi áp dụng công thức. Việc này đòi hỏi sự chính xác trong quá trình tính toán để tránh sai số.

Trong ngành đo đạc địa chính, các chuyên gia thường sử dụng công thức này khi cần xác định diện tích các thửa đất có hình dạng thoi. Họ sử dụng các thiết bị đo góc hiện đại để có được kết quả chính xác nhất.

Hướng dẫn giải bài tập tính diện tích hình thoi từ cơ bản đến nâng cao

Việc tính diện tích hình thoi đòi hỏi nắm vững các công thức cơ bản và phương pháp giải phù hợp với từng dạng bài tập. Công thức tổng quát tính diện tích hình thoi là tích của hai đường chéo chia 2, hoặc tích của cạnh và độ dài đường cao.

Để giải các bài toán về diện tích hình thoi một cách hiệu quả, cần phân tích kỹ dữ kiện đề bài và lựa chọn công thức phù hợp. Tương tự như diện tích hình viên phân, việc áp dụng đúng công thức sẽ giúp giải nhanh và chính xác.

Bài tập tính diện tích hình thoi khi biết hai đường chéo

Đối với dạng bài tập này, công thức áp dụng là S = (d1 x d2)/2, trong đó d1 và d2 là độ dài hai đường chéo. Việc xác định chính xác hai đường chéo là yếu tố then chốt để tìm ra diện tích.

Khi giải loại bài tập này, cần chú ý đơn vị đo của các đường chéo phải thống nhất. Nếu đề bài cho các đơn vị khác nhau, bước đầu tiên là quy đổi về cùng một đơn vị đo.

Một số bài tập có thể yêu cầu tìm đường chéo còn lại khi biết diện tích và một đường chéo. Khi đó, cần vận dụng công thức ngược để tìm ra kết quả.

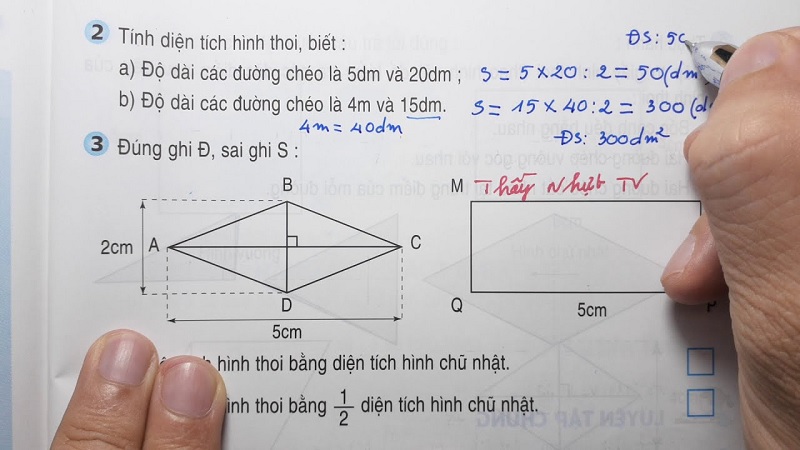
Bài tập tính diện tích hình thoi khi biết cạnh và góc

Với dạng bài tập này, diện tích hình thoi được tính theo công thức S = a² x sinα, trong đó a là độ dài cạnh và α là số đo góc của hình thoi. Việc nắm vững kiến thức về lượng giác là rất quan trọng.

Trong nhiều trường hợp, đề bài có thể cho góc tù thay vì góc nhọn. Lúc này cần áp dụng tính chất của hàm sin để chuyển về góc nhọn tương ứng trước khi tính toán.

Một số bài tập diện tích hình thoi nâng cao có thể kết hợp với các yếu tố khác như đường cao hay đường tròn nội tiếp, ngoại tiếp. Việc phân tích kỹ dữ kiện và vẽ hình phụ sẽ giúp giải quyết bài toán dễ dàng hơn.

Bài tập tổng hợp về diện tích hình thoi

Các bài tập tổng hợp thường kết hợp nhiều yếu tố và đòi hỏi vận dụng linh hoạt các công thức. Việc phân tích bài toán thành các bước nhỏ sẽ giúp giải quyết vấn đề một cách có hệ thống.

Nhiều bài toán yêu cầu tìm các yếu tố phụ trước khi tính được diện tích. Ví dụ như tìm đường cao từ cạnh và góc, hoặc tính độ dài đường chéo từ các yếu tố cho trước.

Một số bài tập có thể liên quan đến tỷ số diện tích giữa hình thoi và các hình khác. Trong trường hợp này, việc thiết lập các phương trình và bất phương trình sẽ giúp tìm ra lời giải chính xác.

Các đặc điểm và tính chất quan trọng của hình thoi trong hình học phẳng

Đặc điểm hình thoi là những yếu tố đặc trưng tạo nên một tứ giác có 4 cạnh bằng nhau. Hình thoi xuất hiện phổ biến trong kiến trúc, thiết kế và nhiều ứng dụng thực tiễn khác. Các tính chất của hình thoi giúp giải quyết nhiều bài toán hình học phức tạp.

Để hiểu rõ về hình thoi, cần phân tích các đặc điểm và tính chất cơ bản của nó thông qua 3 khía cạnh chính: cạnh và góc, đường chéo, và mối quan hệ với diện tích.

Đặc điểm về cạnh và góc của hình thoi

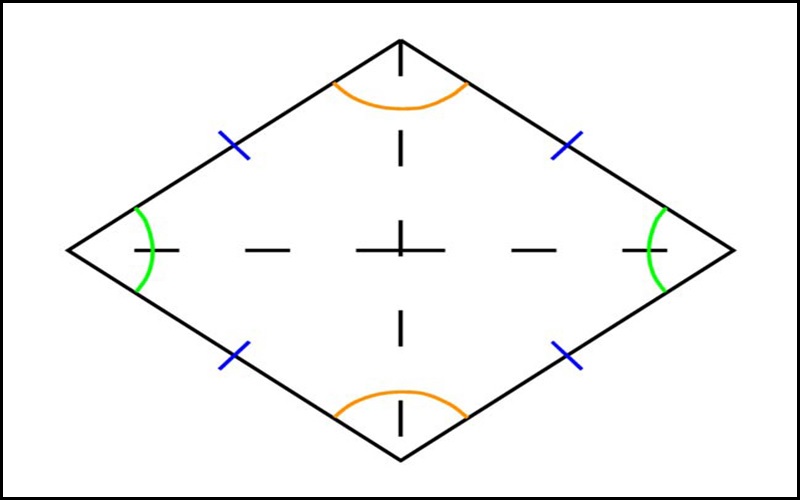
Hình thoi có 4 cạnh bằng nhau là đặc điểm quan trọng nhất phân biệt với các tứ giác khác. Các cạnh kề tạo thành hai cặp góc đối bằng nhau. Góc giữa hai cạnh kề có thể thay đổi nhưng tổng các góc luôn bằng 360 độ.

Trong thực tế, các kiến trúc sư thường sử dụng hình thoi trong thiết kế gạch lát sàn hoặc trang trí tường. Công ty LIXIL đã ứng dụng mẫu gạch hình thoi trong nhiều dự án, tạo hiệu ứng thị giác độc đáo và sang trọng.

Tính chất của đường chéo hình thoi

Hai đường chéo của hình thoi luôn vuông góc và cắt nhau tại trung điểm. Đường chéo chia hình thoi thành 4 tam giác đồng dạng. Điểm giao của hai đường chéo là tâm đối xứng của hình thoi.

Tính chất này được ứng dụng rộng rãi trong diện tích khối cầu và các bài toán hình học không gian phức tạp khác. Các đường chéo còn đóng vai trò quan trọng trong việc tính diện tích hình thoi.

Mối quan hệ giữa diện tích và các yếu tố của hình thoi

Diện tích hình thoi là tích của hai đường chéo chia đôi. Công thức này đơn giản và hiệu quả hơn so với công thức tính diện tích thông thường dựa vào cạnh và góc.

Khi biết độ dài cạnh và góc giữa hai cạnh kề, diện tích hình thoi bằng bình phương cạnh nhân với sin của góc. Mối quan hệ này thể hiện sự liên kết chặt chẽ giữa các yếu tố hình học của hình thoi.

Trong thực tế, các kỹ sư xây dựng thường sử dụng công thức này để tính toán diện tích các cấu trúc hình thoi trong thiết kế mái nhà hoặc các công trình kiến trúc hiện đại.

Ứng dụng thực tiễn của diện tích hình thoi trong đời sống và kiến trúc

Ứng dụng diện tích hình thoi xuất hiện phổ biến trong nhiều lĩnh vực của cuộc sống, từ kiến trúc đến nghệ thuật trang trí. Việc áp dụng các tính chất hình học của hình thoi giúp tối ưu không gian và tạo nên những thiết kế độc đáo. Nắm vững cách tính toán cách tính diện tích hình chóp cụt và diện tích hình thoi là nền tảng quan trọng để ứng dụng vào thực tiễn.

Ứng dụng trong thiết kế và xây dựng

Trong lĩnh vực xây dựng, hình thoi được ứng dụng rộng rãi để thiết kế mái nhà, cửa sổ và các chi tiết kiến trúc. Theo kiến trúc sư John Smith của công ty Architecture Plus, mái nhà hình thoi giúp thoát nước tốt hơn và chịu lực tốt hơn so với các hình dạng thông thường khác.

Các công trình hiện đại thường sử dụng kết cấu dạng lưới hình thoi để tạo độ vững chắc. Ví dụ như tòa nhà 30 St Mary Axe ở London sử dụng hệ thống khung thép hình thoi, vừa đảm bảo tính thẩm mỹ vừa tối ưu khả năng chịu lực của công trình.

Ngoài ra, việc áp dụng Website về môn toán trong tính toán diện tích các mặt hình thoi giúp kiến trúc sư và kỹ sư xây dựng có thể lên kế hoạch sử dụng vật liệu chính xác, tiết kiệm chi phí xây dựng.

Ứng dụng trong nghệ thuật và trang trí

Trong nghệ thuật trang trí nội thất, hình thoi được sử dụng để tạo điểm nhấn và mang lại cảm giác động. Các họa tiết hình thoi trên gạch lát sàn, giấy dán tường tạo hiệu ứng thị giác độc đáo, mang lại chiều sâu cho không gian.

Nghệ sĩ thiết kế Sarah Johnson chia sẻ rằng việc sử dụng các mảng màu hình thoi trong trang trí giúp không gian trở nên sinh động và hiện đại hơn. Các tác phẩm nghệ thuật đương đại thường xuyên sử dụng hình thoi như một yếu tố thẩm mỹ chủ đạo.

Trong thiết kế thời trang, các nhà thiết kế thường xuyên sử dụng họa tiết hình thoi để tạo nên những bộ sưu tập độc đáo. Từ các họa tiết trên vải đến cách cắt may trang phục, hình thoi mang đến sự mới lạ và thu hút trong thời trang đương đại.

Tính diện tích hình thoi là một kỹ năng quan trọng trong hình học phẳng, giúp học sinh nắm bắt và ứng dụng lý thuyết vào thực tế. Thông qua những công thức đa dạng cũng như bài tập sinh động từ cơ bản đến nâng cao, người học có thể dễ dàng giải quyết các nhiệm vụ toán học liên quan. Việc hiểu rõ cách tính diện tích hình thoi không chỉ làm phong phú kiến thức mà còn tạo nền tảng vững chắc cho các môn học sau này.