Diện tích hình vuông được ứng dụng rộng rãi trong toán học cũng như trong đời sống. Trên thực tế sẽ có nhiều cách để tính được diện tích của hình vuông bằng những thông số có sẵn. Bài viết dưới đây sẽ trình bày chi tiết các công thức cũng như bài tập ứng dụng.
Công thức tính diện tích hình vuông
Công thức tính diện tích hình vuông lớp 4 cơ bản nhất như sau:
$$S=a\times a$$
Trong đó S là diện tích hv, a là chiều dài cạnh của hình vuông.
Xem thêm: Hv là gì? Những tính chất của hv?
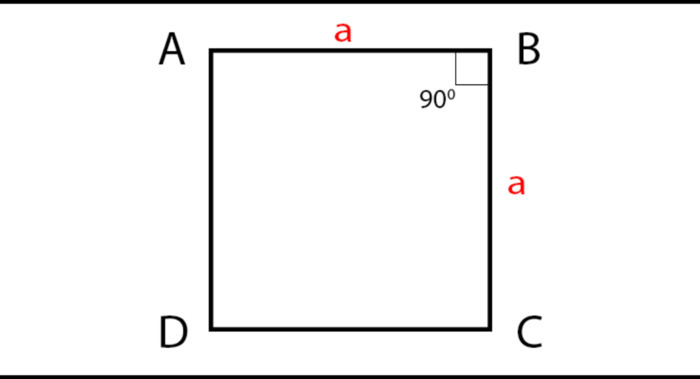
Cách tính diện tích hình vuông từ cơ bản đến nâng cao
Ngoài công thức tính diện tích hình vuông cơ bản như trên, ta còn có thể tính toán dựa trên các số liệu cho sẵn của bài toán theo các công thức sau đây.
Tính diện tích của hình vuông bằng tổng diện tích của 2 tam giác được tạo ra từ một đường chéo
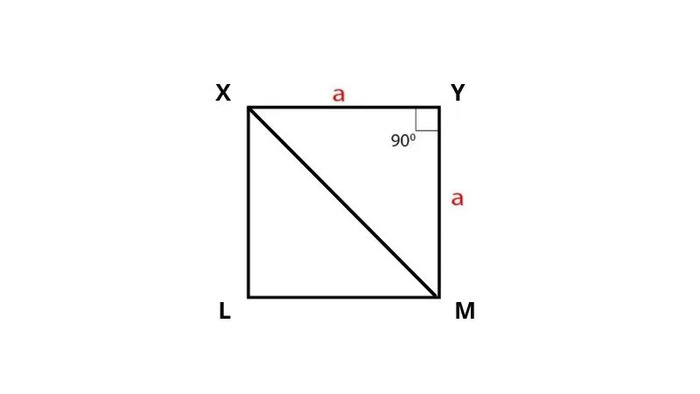
Ta có hình vuông XYML, nếu nối 2 điểm đối diện nhau là X và M sẽ tạo thành đường chéo của hình vuông và có 2 hình tam giác vuông cân là XYM và XLM. Khi đó câu trả lời diện tích hình vuông bằng gì sẽ là tổng diện tích của hai tam giác cân.
Dt hình vuông sẽ như sau:
$$S=\frac12\times a^2+\frac12\times a^2$$
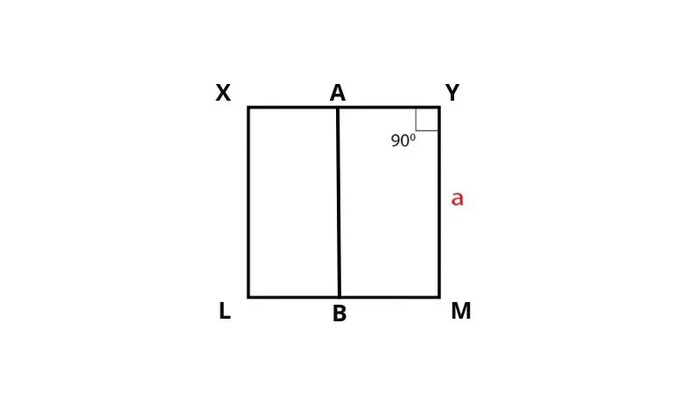
Tính diện tích hình vuông bằng tổng diện tích của 2 hình chữ nhật
Nếu chia hình vuông thành 2 hình chữ nhật như hình minh hoạ, muốn tính diện tích hình vuông thì sẽ bằng tổng diện tích của hai hình chữ nhật đó. Như vậy công thức sẽ là:
$$S=XA\times AB+AY\times AB$$
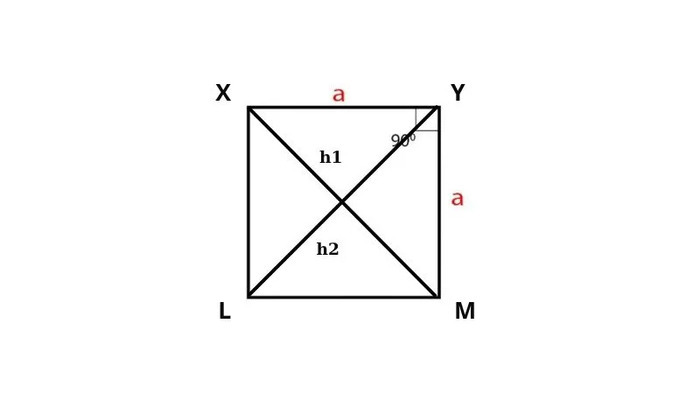
Tính diện tích của hình vuông bằng công thức tính diện tích hình thoi
Hình vuông là một hình thoi đặc biệt vì có 4 góc vuông và 4 cạnh bằng nhau. Do đó công thức tính dt hình thoi cũng được áp dụng để tính với hình vuông. Diện tích khi này được tính như sau:
$$S=\frac12\left(XM+YL\right)$$
Xem thêm: Những cách tính chu vi hình vuông
Một số bài tập minh hoạ về cách tính diện tích hình vuông
Dưới đây là một số ví dụ áp dụng cách tính diện tích hình vuông:
Bài tập 1: Cho một hình thoi ABCD có góc ABC bằng 90 độ, chiều dài của cạnh AB là 5cm. Hỏi diện tích của hình thoi ABCD.
Lời giải:
Hình thoi ABCD có 1 góc vuông, tức là ABCD là hình vuông. Do đó diện tích của ABCD được tính như sau:
$$S=AB^2=5^2=25\;cm^2$$
Bài tập 2: Một mảnh vườn hình vuông có mỗi cạnh là 100dm. Hỏi diện tích của mảnh vườn tính ra m2 là bao nhiêu?
Lời giải:
Ta có 100dm = 10m
Diện tích của mảnh vườn sẽ bằng:
$$S\;=10\times10\;=\;100m^2$$
Bài tập 3: Cho một hình vuông có chu vi là 40cm. Hỏi diện tích của hình đó.
Lời giải:
Chu vi của hình vuông bằng tổng tất cả các cạnh của hình. Mà các cạnh của hình vuông có độ dài bằng nhau. Do đó chiều dài 1 cạnh của hình vuông là 40:4 = 10cm.
Diện tích của hv sẽ bằng: $$S\;=\;10\times10\;=\;100\;cm^2$$
Xem thêm: Các dạng bài toán chứng minh hình vuông
Lưu ý cần biết khi tính dt hình vuông
Trong khi làm bài tập hoặc vận dụng cách để tính được diện tích, bạn sẽ cần chú ý một số vấn đề như sau:
- Các đơn vị của hình khi đề bài giao cần được đổi về cùng một đơn vị như m, cm, dm,…
- Đơn vị đo diện tích hv nói riêng và các hình học khác nói chung đều là cm2, dm2, m2,… Không sử dụng đơn vị đo chiều dài thường như m, cm, dm,…
- Công thức tính diện tích và chu vi hv rất dễ bị nhầm lẫn với nhau. Bạn cần nắm chắc lý thuyết để vận dụng vào thực tế chính xác nhất.
- Hình vuông cũng là hình thang, hình chữ nhật, hình thoi,… Do đó bạn có thể áp dụng công thức tính dt của những hình này cho hình vuông nếu dữ kiện đề bài phù hợp.
Ứng dụng của công thức diện tích hv trong đời sống
Công thức tính dt hình vuông đang được áp dụng rộng rãi trong đời sống. Một số ứng dụng cụ thể được biết đến như sau:
- Trong thiết kế và xây dựng: Diện tích của các bề mặt xây dựng như tường, cửa được áp dụng công thức để tính toán khối lượng nguyên vật liệu cần thiết trong thi công, tránh lãng phí và đảm bảo chính xác nhất.
- Trong trang trí nội thất: Các loại gạch lát, thảm,… được thiết kế theo dạng hình vuông. Nhờ công thức tính diện tích mà có thể tính toán được số lượng, cách bố trí để vừa vặn nhất cho không gian.
- Trong nông nghiệp: Tính diện tích đất đai chính xác sẽ giúp nông dân phân bổ nguồn lực và chuẩn bị hạt giống phù hợp, vừa đủ.
- Trong nghiên cứu và giáo dục: Toán học là bộ môn sử dụng công thức tính dt hình vuông nhiều nhất. Đồng thời công thức cũng được áp dụng trong nghiên cứu ứng dụng hình học và khoa học.

Một số bài tập thực hành tại nhà
Áp dụng các kiến thức trên, dưới đây là một số bài tập thực hành dành cho bạn:
Bài tập 1: Một mảnh vườn hình vuông có chiều dài cạnh là 30m. Nếu mua thêm mỗi cạnh thêm 3m thì diện tích mới của mảnh vườn sẽ tăng thêm bao nhiêu m2?
Hướng dẫn: Áp dụng công thức dt hình vuông, tính dt ban đầu và sau khi tăng cạnh, sau đó lấy dt mới trừ đi dt ban đầu để tìm sự tăng thêm.
Bài tập 2: Để ốp một sàn nhà sẽ cần dùng đến 10 viên gạch men hình vuông, mỗi viên gạch có cạnh dài 50cm. Hãy tính diện tích của sàn nhà đó.
Hướng dẫn: Tính diện tích của một viên gạch men, sau đó nhân với số lượng viên gạch để tìm diện tích sàn nhà.
Bài tập 3: Một miếng đất hình vuông có cạnh là 5m. Tính diện tích của miếng đất đó.
Hướng dẫn: Áp dụng công thức tính diện tích S = axa
Trên đây là bài viết chi tiết về cách để tính diện tích hình vuông. Với những công thức và ví dụ thực tế này, hy vọng tất cả mọi người đều có thể ứng dụng vào thực tế học tập và đời sống. Đừng quên bình luận ngay bên dưới để bày tỏ những ý kiến của bạn nhé!




