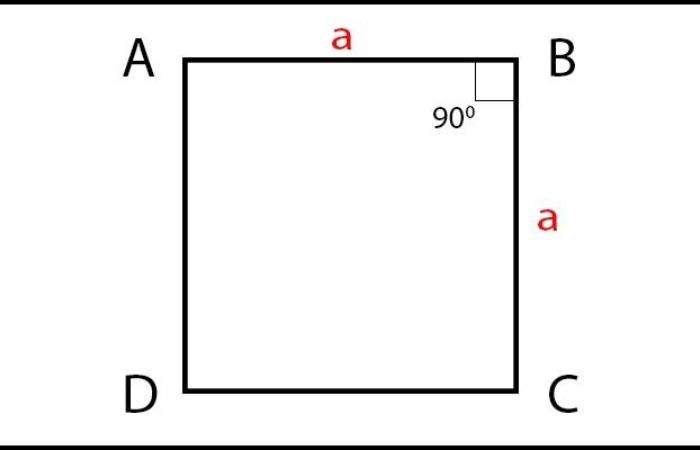
Đường chéo hình thang là một đoạn thẳng được sử dụng thường xuyên khi giải toán hình thang. Để biết rõ tính chất, công thức tính cũng như cách giải các bài tập về đoạn thẳng này, cùng theo dõi thông tin chi tiết trong bài viết dưới đây!
Tính chất đường chéo hình thang
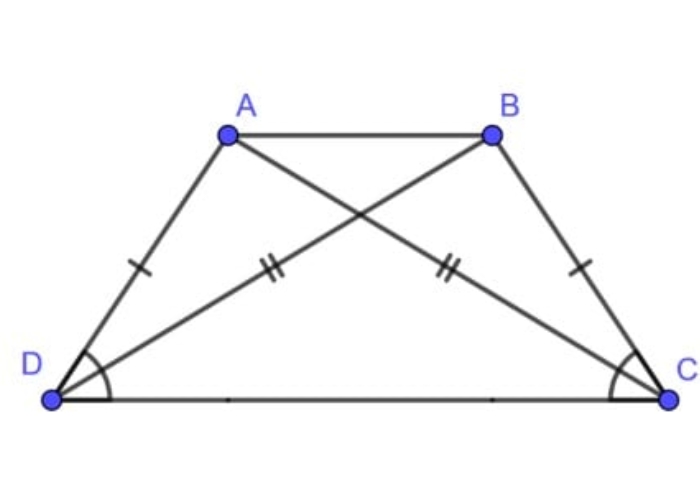
Đường chéo hình thang là một đoạn thẳng kết nối hai đỉnh không kề nhau của hình thang. Đặc biệt, ở hình thang cân, hai đường chéo không chỉ bằng nhau về chiều dài mà còn giao nhau tại đúng trung điểm của mỗi đường.
Trong hình thang, đường chéo là đường thẳng có nhiều tính chất đặc biệt quan trọng, cụ thể:
- Trong ht cân, hai đường chéo có độ dài bằng nhau và cắt nhau ở trung điểm, tạo ra các tam giác đồng dạng.
- Trong ht vuông, đường chéo cắt nhau tạo thành các góc vuông, làm nổi bật tính đối xứng của hình.
- Hai đường chéo chia ht thành hai tam giác vuông đồng dạng, giúp giải quyết các bài toán liên quan đến diện tích và thể tích.
Biết được tính chất đường chéo ht không chỉ giúp chúng ta hiểu rõ hơn về loại hình này mà còn có thể áp dụng vào các vấn đề thực tế như kiến trúc, thiết kế và toán học.
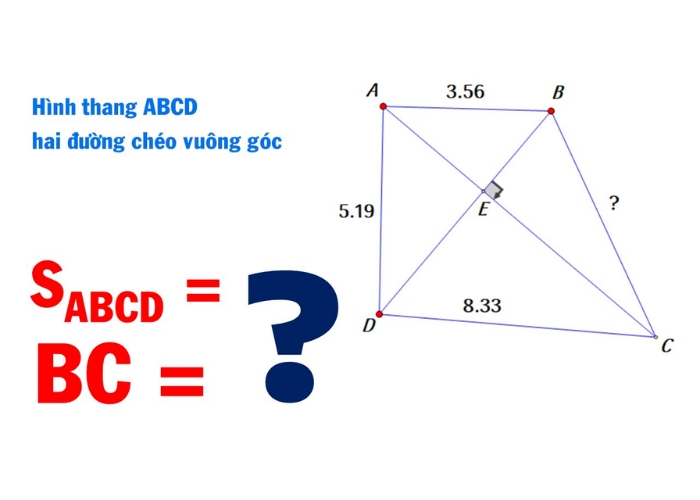
Đọc ngay: Hình thang là gì? Khái niệm, tính chất và dấu hiệu nhận biết
Cách tính đường chéo hình thang đơn giản nhất
Để tính đường chéo hình thang, bạn cần áp dụng đúng công thức cho từng loại hình, cụ thể:
Hình thang vuông
Nếu biết độ dài của hai cạnh bên, ta có thể áp dụng định lý Py-ta-go để tìm độ dài của đường chéo, trong đó a và b là độ dài của hai cạnh bên.
Công thức tính đường chéo hình thang vuông:
$$c=a^2+b^2$$
VD: Cho hình thang vuông ABCD có 2 cạnh bên a = 4 cm, b = 5 cm. Tính đường chéo c của hình.
Giải
Áp dụng công thức tính c hình thang vuông, ta có:
$$\Leftrightarrow a^2+b^2=\Leftrightarrow4^2+5^2=41=6,4cm$$
=> Vậy đường chéo ht vuông ABCD là 6,4 cm.
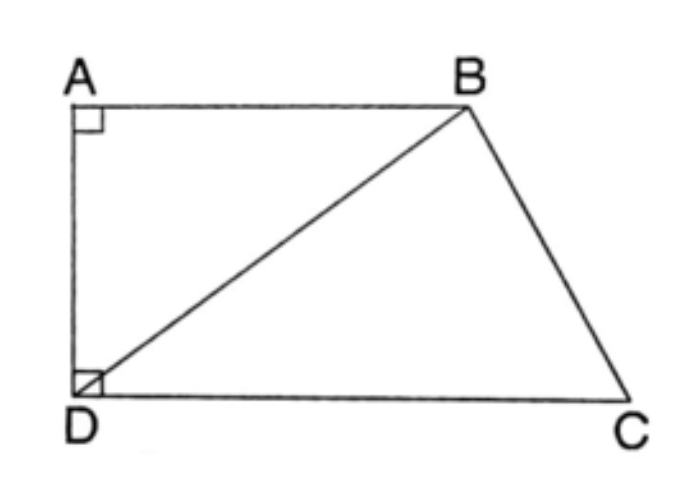
Tham khảo ngay: Cách tính dt hình thang nhanh, đơn giản nhất
Hình thang cân
Trong ht cân, hai đường chéo không chỉ có độ dài bằng nhau mà còn chia hình thành hai tam giác cân đối. Để tính độ dài của mỗi đường chéo, ta có thể sử dụng công thức Pythagoras, dựa trên độ dài của hai đáy và chiều cao của hình thang.
Công thức tính đường chéo hình thang cân:
$$c=h^2+{(\frac{d1+d2}2)}^2$$
VD: Cho hình thang cân ABCD có đáy nhỏ d1 = 5 cm, đáy lớn d2 = 7 cm, độ cao h = 7 cm. Tính đường chéo c của hình.
Giải
Áp dụng công thức tính c hình thang cân, ta có:
$$c=7^2+{(\frac{5+7}2)}^2=\;85\;=\;9,2\;cm\\$$
Đọc thêm: Tổng hợp các công thức tính chu vi hình thang chi tiết nhất
Bài tập minh hoạ cách tính đường chéo hình thang có lời giải
Bài 1: Cho hình thang ABCD với đáy lớn AB = 12 cm, đáy nhỏ CD = 8 cm. Tính độ dài đường chéo của hình.
Giải
Ta có:
AB = a = 12 cm
CD = b = 8 cm
Áp dụng công thức tính c ht vuông, ta có:
$$c=a^2+b^2\\\Leftrightarrow c=12^2+8^2$$
$$\Leftrightarrow\;c\;=\;208\;\;\\=>\;c\;=\;14,42\;cm.$$
Sau khi có c đáy lớn, ta tiếp tục tính c đáy nhỏ bằng cách tương tự: ⇔ c = 11,31 cm.
Đáp số:
- Đường chéo đáy lớn = 14,42 cm
- Đường chéo đáy nhỏ = 11,31cm
Bài 2: Cho hình thang cân ABCD có: AB = 10 cm, CD = 6 cm, h = 8 cm. Tính đường chéo ht cân ABCD.
Giải
Ta có:
- AB = a = 10 cm
- CD = b = 6 cm
- h = 8 cm
Áp dụng công thức ta có:
$$\Leftrightarrow AC=h^2+\;(d1-d2)^2\Leftrightarrow AC=8^2+\;(10-6)^2\Leftrightarrow AC=45\Leftrightarrow AC=8,94cm$$
Vậy đường chéo AC của ht cân ABCD là 8,94 cm.
Ứng dụng của đường chéo hình thang trong thực tế
Đường chéo ht được ứng dụng rộng rãi trong thực tế, cụ thể như sau:
- Định lý Thales: Vận dụng tính chất của đường chéo để chứng minh các đoạn thẳng song song hoặc tính tỷ lệ. Ví dụ, trong các bài toán hình học phức tạp, chúng ta có thể tính độ dài của các đoạn thẳng bằng cách áp dụng định lý Thales vào hình thang.
- Tính đối xứng: Kiểm tra tính đối xứng của các tứ giác dựa trên đường chéo. Cụ thể, đường chéo có thể được sử dụng để xác định tính đối xứng của ht cân hoặc hình bình hành trong các bài toán thiết kế.
- Thiết kế kỹ thuật: Áp dụng cách tính đường chéo trong thiết kế để xác định các yếu tố cân bằng và đối xứng, đặc biệt quan trọng trong kiến trúc và kỹ thuật cơ khí. Ví dụ, trong thiết kế các bộ phận máy hoặc cấu trúc, chúng ta có thể sử dụng tính chất cân bằng của hình thang để đảm bảo tính ổn định và an toàn của sản phẩm.

Tham khảo thêm: Các cách chứng minh hình thang đơn giản dễ hiểu
Bài viết trên đây đã chia sẻ các cách tính đường chéo hình thang và hướng dẫn giải bài tập minh hoạ một cách cụ thể, chi tiết. Đừng quên để lại bình luận nếu bạn vẫn còn thắc mắc về chủ đề này nhé!