Khối cầu là gì, đặc điểm, tính chất và công thức tính diện tích và thể tích, cũng như các ứng dụng thú vị trong đời sống của khối cầu… tất cả những thông tin hữu ích này đều có trong bài viết dưới đây. Khối cầu là một hình dạng ba chiều quen thuộc mà chúng ta thường gặp trong toán học và thế giới tự nhiên. Nó được hình thành từ tất cả các điểm cách đều một điểm cố định gọi là tâm O.
Khối cầu là gì?
Khối cầu là một hình dạng ba chiều được cấu thành bởi tất cả các điểm cách đều một điểm cố định được gọi là tâm (O) một khoảng cách bằng bán kính, được ký hiệu là (r).

Các yếu tố quan trọng hình thành khối cầu bao gồm:
- Tâm (O): Điểm cố định cách đều mọi điểm trên mặt cầu.
- Bán kính (r): Khoảng cách từ tâm (O) đến bất kỳ điểm nào trên mặt cầu.
- Đường kính (d): Đoạn thẳng đi qua tâm (O) và nối hai điểm đối diện trên mặt cầu. d=2r
- Mặt cầu: Bề mặt cong bao quanh khối cầu.
Đặc điểm của khối cầu
Khối cầu có những đặc điểm hình học dễ nhận dạng như sau:
- Đường bao quanh của khối cầu được gọi là mặt cầu, nó có dạng của một mặt cong kín, mặt cầu không có đỉnh hay cạnh.
- Mọi điểm trên mặt cầu đều cách tâm (O) của khối cầu một khoảng cách bằng bán kính (r).
- Diện tích mặt cầu: S = 4πr2
- Thể tích khối cầu: V = 4/3πr3
- Khối cầu có tính chất đối xứng trục và đối xứng tâm.
- Khối cầu có thể lăn được trên mặt phẳng.
Ứng dụng của khối cầu trong thực tế
Trong cuộc sống hàng ngày, không quá khó để chúng ta bắt gặp hình ảnh của một vật có dạng khối cầu. Hình dạng này có nhiều ứng dụng thú vị trong thực tế có thể kể đến như:
- Xây dựng: Vòm cầu từ khối cầu được sử dụng để xây dựng các công trình như nhà thờ, sân vận động, cầu cống,… Vòm cầu có khả năng chịu lực cao và tiết kiệm vật liệu xây dựng…
- Kỹ thuật: Khối cầu được sử dụng trong nhiều bộ phận của máy móc như bánh răng, trục, ổ bi,… Khối cầu giúp giảm ma sát và tăng hiệu quả hoạt động của máy móc.
- Nghệ thuật: Khối cầu là hình dạng cơ bản của nhiều tác phẩm điêu khắc. Các nhà điêu khắc sử dụng khối cầu để thể hiện các hình dạng khác nhau như con người, động vật, và các vật thể khác.
- Khoa học: Các nhà khoa học sử dụng mô hình khối cầu để nghiên cứu các hành tinh, sao, và các thiên thể khác trong vũ trụ. Ngoài ra, khối cầu còn được sử dụng để mô phỏng các hiện tượng tự nhiên như sự lan truyền sóng âm, sự di chuyển của chất lỏng,…
- Y học: Khối cầu được sử dụng để cấy ghép các bộ phận cơ thể như khớp hông, khớp gối,… Khối cầu giúp thay thế các bộ phận bị tổn thương của con người và cải thiện khả năng vận động của cơ thể.
- Thể thao: Quả bóng đá, bóng rổ, bóng chuyền… có hình dạng khối cầu, là vật dụng không thể thiếu trong các môn thể thao phổ biến.
- Giải trí: Khối cầu được sử dụng trong nhiều trò chơi như bi da, bi ve, trò chơi bowling…
Tính chất của khối cầu
Khối cầu có những tính chất quan trọng giúp chúng ta giải những bài toán hình học, điển hình như:
Tính chất về mặt hình học
Tính chất về mặt hình học của khối cầu bao gồm:
- Mọi điểm trên mặt cầu đều cách tâm (O) một khoảng cách bằng bán kính (r).
- Đường kính (d) của khối cầu bằng hai lần bán kính (r): d = 2r.
- Hai điểm bất kỳ trên mặt cầu đều cách nhau một khoảng cách không nhỏ hơn đường kính (d).
- Đối xứng trục: Khối cầu có tính chất đối xứng qua mọi đường thẳng đi qua tâm (O) của nó.
- Đối xứng tâm: Khối cầu có tính chất đối xứng tâm qua tâm (O) của nó.
- Tiếp tuyến: Mỗi điểm tuỳ ý trên một mặt cầu chỉ có duy nhất một đường tiếp tuyến đi qua tại điểm đó. Góc tạo bởi đường tiếp tuyến và bán kính của khối cầu bằng 90 độ.
Tính chất về vị trí tương đối
Vị trí tương đối giữa mặt phẳng và khối cầu:
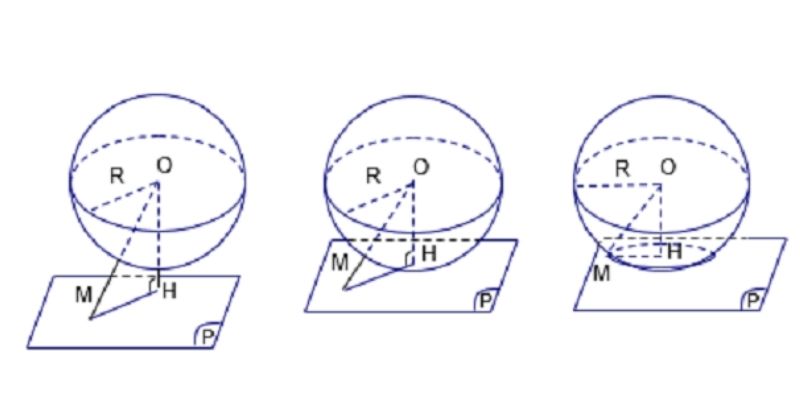
- Mặt phẳng cắt khối cầu: Khi mặt phẳng cắt khối cầu theo một đường cong kín, ta nói mặt phẳng cắt khối cầu.
- Mặt phẳng tiếp xúc với khối cầu: Khi mặt phẳng chỉ cắt khối cầu tại một đường tròn, ta nói mặt phẳng tiếp xúc với khối cầu.
- Mặt phẳng song song với mặt cầu: Khi mặt phẳng và mặt cầu không có điểm chung nào, ta nói mặt phẳng song song với mặt cầu.
 Vị trí tương đối của hai khối cầu:
Vị trí tương đối của hai khối cầu:
Vị trí tương đối của hai khối cầu được xác định bởi vị trí của các tâm và bán kính của chúng. Hai khối cầu có thể nằm trong ba trạng thái tương đối với nhau:
- Tiếp xúc ngoài: Khi hai tâm cách nhau một khoảng bằng tổng bán kính của hai khối cầu.
- Tiếp xúc trong: Khi hai tâm cách nhau một khoảng bằng hiệu số bán kính của hai khối cầu (bán kính lớn hơn trừ bán kính nhỏ hơn).
- Cắt nhau: Khi hai tâm cách nhau một khoảng nhỏ hơn tổng bán kính và lớn hơn hiệu số bán kính của hai khối cầu.
Tính chất khác
Ngoài ra, khối cầu còn có một số tính chất khác như:
- Trục đối xứng của khối cầu: là đường thẳng đi qua tâm (O) của nó, sao cho mọi điểm trên mặt cầu đều cách đều hai mặt phẳng đối xứng được tạo ra bởi đường thẳng đó khi quay quanh tâm (O).
- Tâm đối xứng của khối cầu: là điểm (O) nằm trên trục đối xứng của nó, sao cho mọi điểm trên mặt cầu đều cách đều hai mặt phẳng đối xứng được tạo ra bởi trục đối xứng đó khi quay quanh tâm (O).
- Mặt phẳng đối xứng của khối cầu: là mặt phẳng đi qua tâm (O) của nó, sao cho mọi điểm trên mặt cầu đều cách đều hai mặt phẳng đối xứng được tạo ra bởi mặt phẳng đó khi quay quanh tâm (O).
- Khối cầu có số cạnh bằng 0, số đỉnh bằng 0 và số mặt bằng 1.
- Khối cầu có thể lăn được trên mặt phẳng.
- Khối cầu có thể nội tiếp hoặc ngoại tiếp một khối cầu khác.
Khối cầu nội tiếp, khối cầu ngoại tiếp là gì?
Nhắc đến khái niệm khối cầu là gì, ta thường nghe đến 2 khái niệm trong hình học đó là: khối cầu nội tiếp và khối cầu ngoại tiếp.
 Khối cầu nội tiếp là gì?
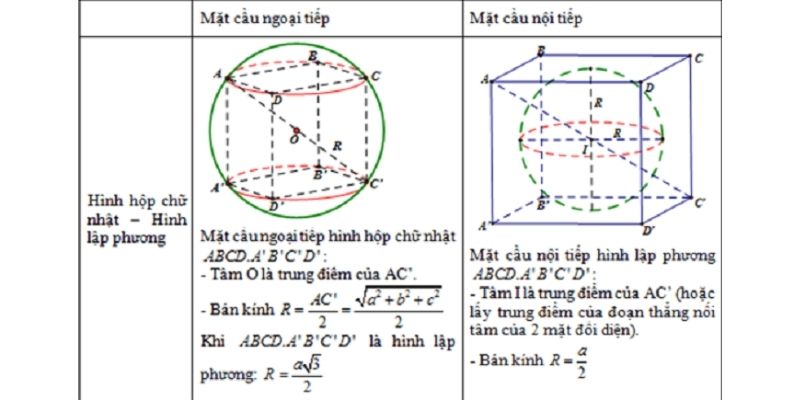
Khối cầu nội tiếp là gì?
Khối cầu nội tiếp một đa diện là khối cầu nằm hoàn toàn bên trong đa diện đó và tiếp xúc với tất cả các mặt của đa diện tại một điểm.
Đặc điểm của khối cầu nội tiếp:
- Bán kính của khối cầu nội tiếp đa diện luôn nhỏ hơn hoặc bằng bán kính đường tròn ngoại tiếp đa diện đó.
- Tâm của khối cầu nội tiếp đa diện luôn nằm trên các đường phân giác của các góc nhọn trong đa diện đó.
Công thức tính bán kính:
- Đối với đa diện lồi: rn=A3V
- rn: Bán kính khối cầu nội tiếp
- V: Thể tích đa diện
- A: Diện tích mặt ngoài đa diện
- Đối với đa diện bất kỳ: rn ≤ A3V
Khối cầu ngoại tiếp:
Khối cầu ngoại tiếp một đa diện là khối cầu bao quanh đa diện đó và tiếp xúc với đa diện tại ít nhất một điểm.
Đặc điểm của khối cầu ngoại tiếp:
- Bán kính của khối cầu ngoại tiếp đa diện luôn lớn hơn hoặc bằng bán kính đường tròn ngoại tiếp đa diện đó.
- Tâm của khối cầu ngoại tiếp đa diện có thể nằm bất kỳ đâu trong không gian.
Công thức tính bán kính:
- Đối với đa diện lồi: re=2a
- re: Bán kính khối cầu ngoại tiếp
- a: Độ dài cạnh dài nhất của đa diện
- Đối với đa diện bất kỳ: re≥2a
Lời kết
Hy vọng rằng bài viết trên đây của chúng tôi đã cung cấp cho bạn những thông tin hữu ích về khối cầu là gì, đặc điểm, tính chất và ứng dụng của nó trong đời sống như thế nào. Hiểu biết về khối cầu có thể giúp ích rất nhiều cho chúng ta trong việc học tập, nghiên cứu cũng như một số công việc đặc thù.




