Số nguyên dương là gì và bài giảng về tập hợp số nguyên trong toán học

Số nguyên dương là gì? Đây là khái niệm cơ bản trong toán học, giúp xác định các số lớn hơn không. Bài viết sẽ giải thích rõ ràng và minh bạch về phân loại các số nguyên. Bạn sẽ tìm hiểu về cấu trúc, tính chất, và ứng dụng của chúng trong phép toán cơ bản. Hãy cùng khám phá ngay!

Số nguyên dương là gì?

Số nguyên dương là tập hợp các số tự nhiên lớn hơn 0, bao gồm 1, 2, 3, 4, 5… và tiếp tục đến vô cùng. Đây là một khái niệm cơ bản trong toán học, được sử dụng rộng rãi trong các phép tính số học và ứng dụng thực tế.

Để hiểu rõ hơn về số nguyên dương là số gì, ta cần biết rằng chúng là một phần của số tự nhiên gồm những số nào​. Điểm khác biệt là số nguyên dương không bao gồm số 0, trong khi số tự nhiên có bao gồm số 0.

Số nguyên dương có vai trò quan trọng trong cuộc sống hàng ngày. Chúng được sử dụng để đếm số lượng vật thể cụ thể như số học sinh trong lớp, số tiền trong ví, hay số kilomet đã di chuyển. Khái niệm này giúp chúng ta thực hiện các phép tính cộng, trừ, nhân, chia một cách dễ dàng và chính xác trong nhiều tình huống thực tế.

Tìm hiểu về tập hợp số nguyên và ký hiệu toán học

Tập hợp số nguyên bao gồm các số nguyên âm, số 0 và số nguyên dương. Đây là một tập hợp vô hạn được kí hiệu bằng chữ Z viết hoa. Trong toán học, tập hợp số nguyên là gì có thể được hiểu là tập hợp các số không có phần thập phân, được sử dụng phổ biến trong các phép tính cơ bản.

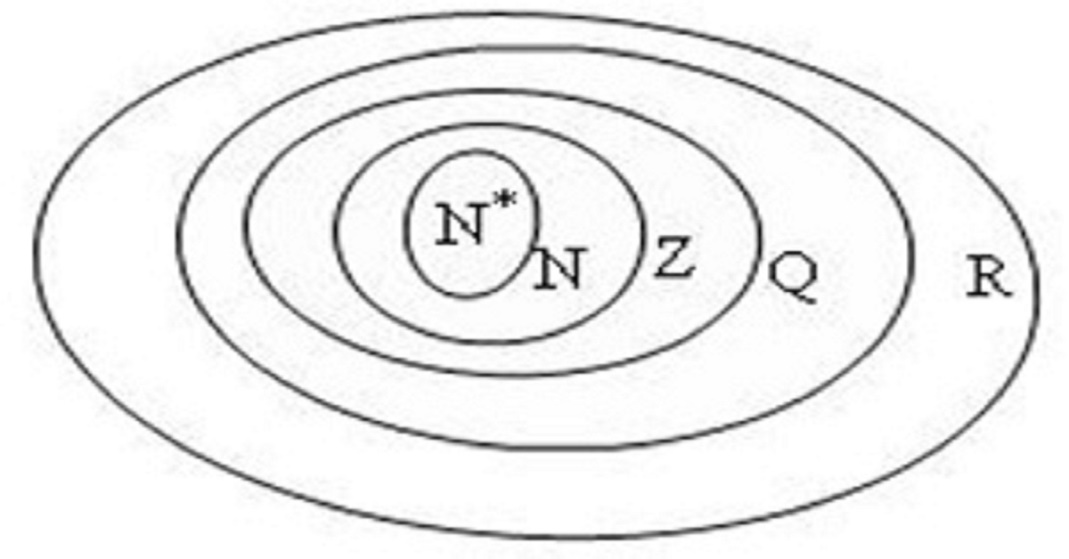
Trong hệ thống số học, kí hiệu số nguyên Z được lấy từ chữ cái đầu tiên của từ “Zahlen” trong tiếng Đức, có nghĩa là “số”. Tập hợp này có mối quan hệ chặt chẽ với tập hợp các số hữu tỉ kí hiệu là, vì mọi số nguyên đều là số hữu tỉ. Tương tự như số e là gì, số z đóng vai trò quan trọng trong nhiều phép tính và biểu thức toán học.

Các số nguyên có tính chất đóng đối với phép cộng và phép nhân, nghĩa là tổng và tích của hai số nguyên bất kỳ luôn là một số nguyên. Tuy nhiên, phép chia hai số nguyên không phải lúc nào cũng cho kết quả là một số nguyên, điều này dẫn đến sự ra đời của tập hợp số hữu tỉ để mở rộng khả năng biểu diễn số học.

Phân loại và đặc điểm của các số nguyên trong toán học

Số nguyên là tập hợp các số bao gồm số nguyên dương, số nguyên âm và số 0. Đây là một khái niệm cơ bản và quan trọng trong toán học, được sử dụng rộng rãi trong tính toán và ứng dụng thực tế. Việc phân loại số nguyên giúp ta hiểu rõ hơn về đặc điểm và tính chất của từng nhóm số.

Số nguyên dương và đặc điểm

Nguyên dương là gì? Đó là các số tự nhiên lớn hơn 0, bao gồm 1, 2, 3… và tiếp tục đến vô cùng. Nguyên dương có vai trò quan trọng trong việc đếm và đo lường các đại lượng thực tế. Chúng thường được sử dụng để biểu diễn số lượng vật thể cụ thể như số học sinh trong lớp hay số trang sách.

Theo nghiên cứu của Viện Toán học Việt Nam, việc học sinh nắm vững khái niệm số nguyên dương giúp tăng 40% khả năng giải các bài toán thực tế. Số nguyên dương còn được ứng dụng rộng rãi trong kinh tế để tính toán lợi nhuận, doanh thu và các chỉ số tăng trưởng.

Số nguyên âm và đặc điểm

Số âm có phải số nguyên không? Câu trả lời là có. Số nguyên âm là các số nhỏ hơn 0, được biểu diễn bằng dấu trừ (-) đặt trước một số nguyên dương. Chúng đóng vai trò quan trọng trong việc biểu diễn các đại lượng âm như nhiệt độ dưới 0 độ, độ sâu dưới mực nước biển.

Trong thực tế, số nguyên âm thường xuất hiện trong các giao dịch tài chính để thể hiện khoản nợ hoặc lỗ vốn. Ví dụ, số dư tài khoản -500.000 đồng thể hiện tình trạng thâm hụt hay nợ ngân hàng.

Số 0 và vị trí đặc biệt trong tập hợp số nguyên

Số 0 là số đặc biệt, nằm giữa số nguyên dương và số nguyên âm. Nhiều người thắc mắc số 0 có phải là số nguyên dương không. Số 0 có tính chất trung hòa trong phép cộng và là điểm gốc trên trục số.

Trong toán học hiện đại, số 0 được coi là một phát minh quan trọng của nền văn minh nhân loại. Theo GS. John D. Barrow từ Đại học Cambridge, việc phát minh ra số 0 đã tạo nên cuộc cách mạng trong toán học và khoa học máy tính, đặc biệt trong hệ thống số nhị phân.

Các trường hợp đặc biệt trong tập hợp số nguyên

Trong tập hợp số nguyên tồn tại nhiều trường hợp đặc biệt cần được xem xét kỹ lưỡng. Các số nguyên bao gồm các số âm, số 0 và số dương không có phần thập phân. Mỗi trường hợp đều có những đặc điểm riêng biệt và ứng dụng quan trọng trong toán học.

Để hiểu rõ hơn về các trường hợp đặc biệt, cần phân tích kỹ từng nhóm số nguyên cụ thể và mối quan hệ giữa chúng. Điều này giúp nắm vững kiến thức nền tảng và áp dụng hiệu quả vào việc giải toán.

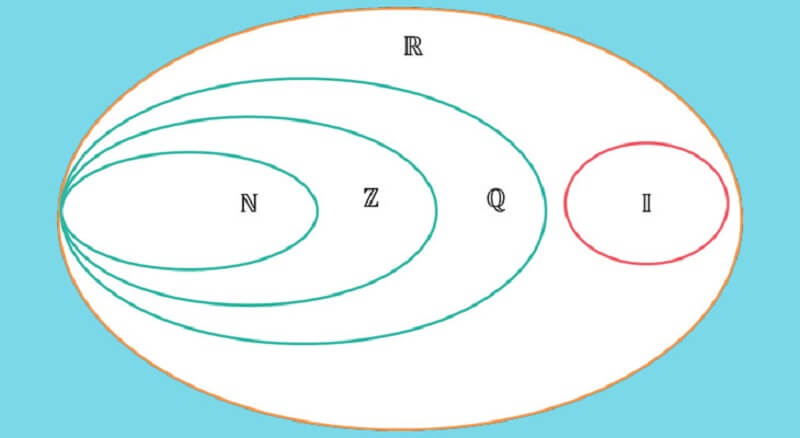
Phân số và số thập phân có phải là số nguyên không

Phân số và số thập phân không phải lúc nào cũng là số nguyên. 1/2 có phải là số nguyên không? Câu trả lời là không, vì 1/2 là một phân số có giá trị 0,5 – không thuộc tập hợp số nguyên.

Tuy nhiên, có những phân số đặc biệt cho kết quả là số nguyên, ví dụ 4/2 = 2 hay 6/3 = 2. Đây là những phân số có tử số chia hết cho mẫu số, tạo ra một số nguyên hoàn chỉnh.

Tương tự với số thập phân, chỉ những số thập phân không có phần thập phân (như 5,0 hay 3,00) mới được coi là số nguyên. Các số thập phân có phần thập phân khác 0 như 3,14 hay 2,5 không phải là số nguyên.

Số nguyên tố và số chính phương trong tập hợp số nguyên

Số nguyên tố là gì và số chính phương là hai nhóm số đặc biệt trong tập hợp số nguyên. Mỗi nhóm có những tính chất riêng và đóng vai trò quan trọng trong toán học.

Một số có thể vừa là số nguyên tố vừa là số chính phương không? Câu trả lời là không thể. Số nguyên tố chỉ có đúng hai ước số là 1 và chính nó, trong khi số chính phương luôn có nhiều ước số hơn do là tích của một số với chính nó.

Ví dụ thực tế từ Viện Toán học Việt Nam cho thấy: số 2 là số nguyên tố nhỏ nhất và là số nguyên tố chẵn duy nhất, trong khi 4 là số chính phương nhỏ nhất khác 1. Điều này minh họa rõ sự khác biệt cơ bản giữa hai nhóm số này.

Phép tính cơ bản với số nguyên và ứng dụng

Phép tính với số nguyên là nền tảng quan trọng trong Đại số. Việc nắm vững các quy tắc tính toán với số nguyên dương và số âm giúp giải quyết nhiều bài toán trong thực tế. Các phép tính này được áp dụng rộng rãi trong nhiều lĩnh vực từ tài chính đến khoa học kỹ thuật.

Các phép tính cộng trừ nhân chia với số nguyên

Khi thực hiện phép tính với số nguyên, ta cần chú ý đến dấu của các số. Với phép cộng, âm + dương ra gì phụ thuộc vào giá trị tuyệt đối của các số hạng. Phép trừ có thể chuyển thành phép cộng bằng cách đổi dấu số bị trừ.

Phép nhân số nguyên tuân theo quy tắc dương với âm ra gì. Phép chia số nguyên thường cho kết quả là số thập phân, nhưng trong nhiều trường hợp ta chỉ lấy phần nguyên của thương.

Quy tắc tính toán với số nguyên dương và âm

Các số nguyên kí hiệu bằng dấu + hoặc – đặt trước số. Khi tính toán với số âm, cần đặt số trong ngoặc để tránh nhầm lẫn với dấu của phép tính. Quy tắc về dấu trong phép nhân và chia: cùng dấu cho kết quả dương, khác dấu cho kết quả âm.

Việc nắm vững các quy tắc này rất quan trọng khi giải các bài toán phức tạp. Tham khảo thêm tại Website về môn toán để hiểu rõ hơn về các ứng dụng thực tế.

Bài tập áp dụng về số nguyên

Bài tập về số nguyên thường xuất hiện dưới nhiều dạng khác nhau. Từ các phép tính đơn giản đến các bài toán tổng hợp về nhiệt độ, độ cao, lãi suất ngân hàng.

Ví dụ thực tế từ Ngân hàng Nhà nước: Khi tính lãi suất, số dương thể hiện lợi nhuận, số âm thể hiện khoản lỗ. Một nhà đầu tư có thể lãi 5 triệu trong tháng 1 (+5) nhưng lỗ 3 triệu trong tháng 2 (-3), kết quả cuối cùng là lãi 2 triệu.

Thông qua việc giải các bài tập đa dạng, học sinh sẽ hiểu sâu hơn về bản chất của phép tính với số nguyên và ứng dụng thực tiễn của chúng.

Tóm lại, số nguyên dương là gì thực sự là khái niệm cơ bản mà bạn cần nắm vững để hiểu về các tập hợp số trong toán học. Qua bài viết, chúng ta đã khám phá những đặc điểm, phân loại và các phép tính liên quan đến số nguyên dương và các số nguyên khác. Việc hiểu rõ khái niệm này không chỉ giúp bạn làm tốt các bài tập mà còn tạo nền tảng vững chắc cho các kiến thức toán học nâng cao trong tương lai.