Nghiệm tầm thường là gì? Đây là một khái niệm quan trọng trong lý thuyết phương trình, đặc biệt là trong nghiên cứu về phương trình vi phân và đại số tuyến tính. Tác động toàn diện việc phân tích các hệ thống toán học và vật lý…
Nghiệm tầm thường, nghiệm không tầm thường là gì?
Trước tiền chúng ta sẽ cùng nhau tìm câu trả lời cho câu hỏi nghiệm tầm thường là gì? Nghiệm không tầm thường là gì?
Khái niệm nghiệm tầm thường
Nghiệm tầm thường là một giải pháp của một phương trình hoặc hệ phương trình mà tất cả các biến đều bằng 0. Nói cách khác, nghiệm tầm thường là khi không có biến nào trong phương trình có giá trị khác 0. Nó còn được gọi là nghiệm hiển nhiên, nghiệm đơn vị, nghiệm null.
Ví dụ:
- Phương trình: 2x + 3y = 6
- Nghiệm tầm thường: x = 0, y = 0
- Hệ phương trình:
2x + y = 4
3x + 2y = 7- Nghiệm tầm thường: x = 0, y = 0

Khái niệm nghiệm không tầm thường
Nghiệm không tầm thường là một giải pháp của một phương trình hoặc hệ phương trình mà ít nhất một biến có giá trị khác 0. Nói cách khác, nghiệm không tầm thường là khi không phải tất cả các biến trong phương trình hoặc hệ phương trình đều bằng 0.
Ví dụ:
- Phương trình: 2x + 3y = 6
- Nghiệm không tầm thường: x = 1, y = 1
- Hệ phương trình:
2x + y = 4
3x + 2y = 7- Nghiệm không tầm thường: x = 1, y = 2
So sánh nghiệm tầm thường và nghiệm không tầm thường
Sau khi đã nắm rõ nghiệm tầm thường là gì, nghiệm không tầm thường là gì. Chúng ta sẽ cùng nhau đi tìm hiểu sự khác biệt của hai loại nghiệm này.
Định nghĩa
- Nghiệm tầm thường thường là nghiệm hiển nhiên, dễ thấy nhất của phương trình, thường có dạng đơn giản như 0 hoặc vector 0.
- Nghiệm không tầm thường là các nghiệm khác 0 hoặc các nghiệm phức tạp hơn, thường đòi hỏi các phương pháp giải phức tạp hơn để tìm ra.
Ý nghĩa toán học
- Nghiệm tầm thường thường tương ứng với trạng thái cân bằng hoặc không có sự thay đổi trong hệ thống.
- Nghiệm không tầm thường thường mô tả các trạng thái hoặc hành vi thú vị hơn của hệ thống.
Phương pháp tìm
- Nghiệm tầm thường thường có thể được xác định bằng cách kiểm tra trực tiếp hoặc bằng trực giác.
- Nghiệm không tầm thường thường đòi hỏi các kỹ thuật giải phương trình phức tạp hơn.

Trong phương trình vi phân
Nghiệm tầm thường thường là hằng số, như y = 0. Ngược lại, nghiệm không tầm thường là các hàm phụ thuộc vào biến độc lập. Ngoài ra, nghiệm tầm thường, mặc dù đơn giản, có thể quan trọng trong việc hiểu cấu trúc cơ bản của hệ thống. Trong khi nghiệm không tầm thường thường cung cấp thông tin có giá trị hơn về hành vi và đặc tính của hệ thống trong các tình huống thực tế.
Tính chất của nghiệm tầm thường
Bên cạnh khái niệm nghiệm tầm thường là gì? Những tính chất của loại nghiệm này cũng thu hút mối quan tâm của không ít người.
Tính tồn tại
Nghiệm tầm thường luôn tồn tại cho mọi hệ phương trình tuyến tính thuần nhất. Bất kể hệ số của phương trình như thế nào, vector 0 (tất cả các thành phần đều bằng 0) luôn là một nghiệm.
Tính duy nhất
Trong một số trường hợp, nghiệm tầm thường có thể là nghiệm duy nhất của phương trình thuần nhất. Điều này xảy ra khi ma trận hệ số của hệ phương trình có định thức khác 0 (ma trận khả nghịch).
Tính bất biến tuyến tính
Nếu áp dụng bất kỳ phép biến đổi tuyến tính nào lên nghiệm tầm thường, kết quả vẫn là nghiệm tầm thường. Điều này phản ánh tính chất cơ bản của không gian vector.
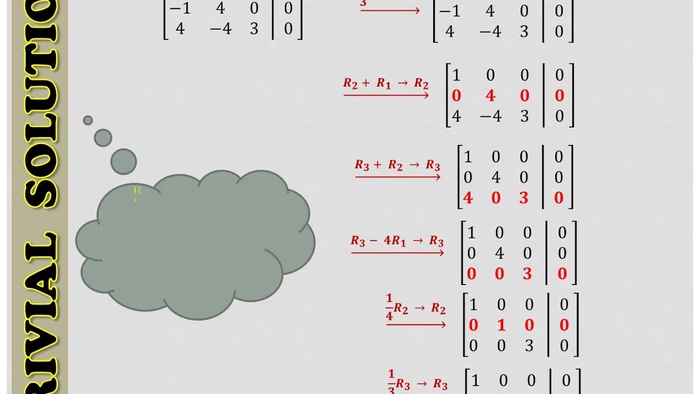
Tính liên tục và độc lập tuyến tính
Trong lý thuyết về phương trình vi phân, nghiệm tầm thường thường tương ứng với hàm hằng số, thể hiện tính liên tục và ổn định. Nghiệm tầm thường luôn độc lập tuyến tính với mọi nghiệm không tầm thường khác của phương trình.
Ứng dụng của nghiệm tầm thường
Nghiệm tầm thường có nhiều ứng dụng quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật. Dưới đây là một số ứng dụng chính:
- Phân tích ổn định: Trong lý thuyết hệ thống động, nghiệm tầm thường thường đại diện cho điểm cân bằng.
- Vật lý học: Trong cơ học, nghiệm tầm thường có thể biểu thị trạng thái nghỉ của một hệ. Trong điện từ học, nó có thể đại diện cho trường không có điện tích hoặc dòng điện.
- Sinh học toán học: Trong mô hình tăng trưởng quần thể, nghiệm tầm thường thường tương ứng với quần thể có kích thước bằng 0, giúp nghiên cứu các điều kiện dẫn đến sự tuyệt chủng.
- Kinh tế học: Trong các mô hình kinh tế, nghiệm tầm thường có thể biểu thị trạng thái cân bằng của thị trường hoặc điểm mà không có tăng trưởng kinh tế.
- Lý thuyết điều khiển: Nghiệm tầm thường được sử dụng để thiết kế các hệ thống điều khiển, đặc biệt trong việc ổn định hệ thống xung quanh một điểm hoạt động mong muốn.
- Hóa học: Trong động học phản ứng, nghiệm tầm thường có thể biểu thị trạng thái cân bằng hóa học hoặc điểm mà không có phản ứng xảy ra.
- Khoa học máy tính: Trong học máy và tối ưu hóa, nghiệm tầm thường thường được sử dụng như một điểm khởi đầu cho các thuật toán tìm kiếm hoặc tối ưu hóa.
Lời kết
Tóm lại, sau khi hiểu rõ nghiệm tầm thường là gì, ta dễ dàng nhận ra nó đóng vai trò quan trọng trong nhiều lĩnh vực của toán học, khoa học và kỹ thuật. Nó không chỉ là một khái niệm cơ bản trong lý thuyết phương trình, mà còn là một công cụ hữu ích trong việc phân tích và hiểu biết các hệ thống phức tạp.