Lượng giác hóa số phức là một chủ đề quan trọng trong toán học, đóng vai trò nền tảng cho nhiều lĩnh vực khác nhau như giải tích phức, hình học phức, và ứng dụng trong điện tử, vật lý,… Đây là một dạng bài tập thường xuyên xuất hiện trong đề thi THPT quốc gia. Bài viết dưới đây của Hocthenao.vn sẽ cung cấp toàn bộ lý thuyết trọng tâm, bài tập vận dụng, giúp các bạn có thể đạt được điểm số tối đa trong phần này.
Lượng giác hoá số phức là gì?
Lượng giác hóa số phức là phương pháp biến đổi số phức sang dạng lượng giác, qua đó giúp dễ dàng tính toán, biểu diễn trong không gian phức. Quá trình lượng giác hóa số phức bao gồm xác định góc pha và mô đun của số phức, cuối cùng có thể biểu diễn giúp hình dung trực quan hơn.
Như chúng ta đã biết, dạng z = a + bi (với a, b thuộc R) được gọi là dạng đại số của số phức z. Trong khi đó, dạng lượng giác hoá của số phức được phát biểu như sau: Số phức z được gọi là số phức dạng lượng giác nếu nó được biểu diễn dưới dạng:
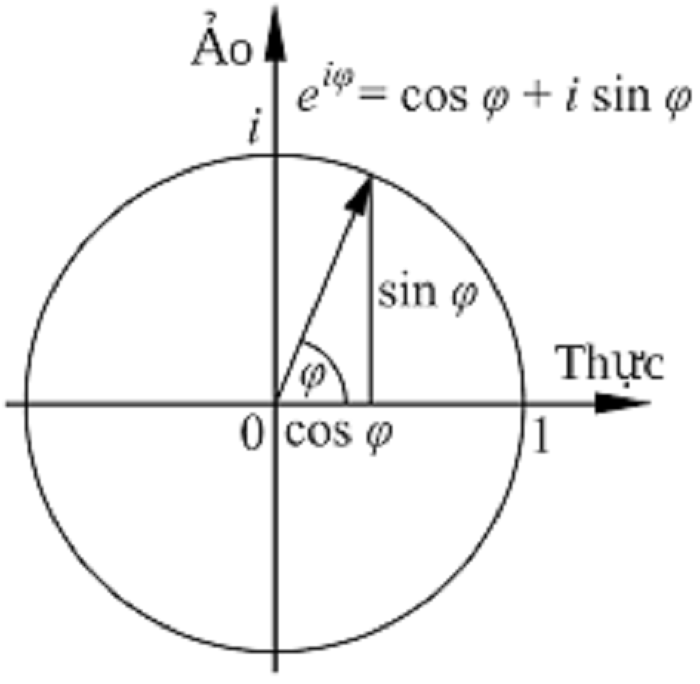
z=r(cosφ+isinφ)
Trong đó: r là mô đun tuyệt đối (độ lớn) của số phức z, φ là góc lượng giác (acgumen) của số phức z.
Argument của số phức là gì?
Argument (hay còn gọi là góc lượng giác) của số phức là một khái niệm quan trọng trong toán học, đóng vai trò thiết yếu trong việc biểu diễn và thao tác với số phức dạng lượng giác. Định nghĩa Argument của số phức được phát biểu như sau:
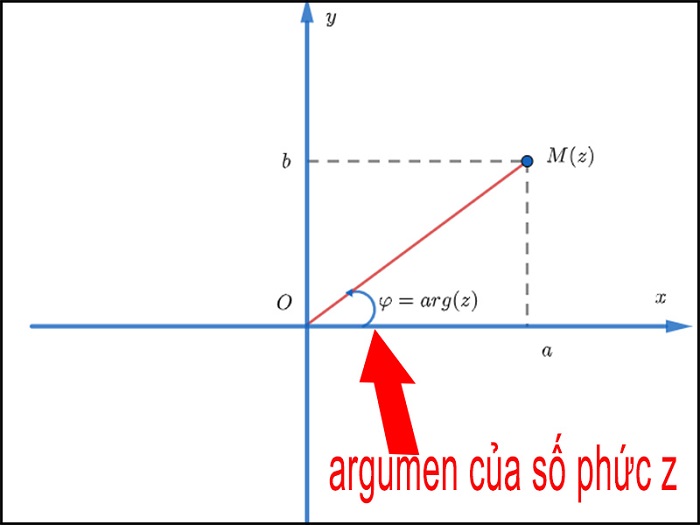
Cho số phức z=a+bi (a, b là số thực) và z≠0. Gọi M là điểm trong mặt phẳng phức biểu diễn số phức z. Argument của z, ký hiệu là φ, được định nghĩa là số đo góc (theo đơn vị radian) giữa trục thực dương Ox và tia OM.
Từ acgumen φ và mô đun r (độ lớn) của số phức z, ta có thể biểu diễn z dưới dạng lượng giác:
z = r(cosφ+isinφ)
Tính chất:
-
- Argument của một số phức khác 0 không duy nhất. Hai số phức z1 và z2 có cùng mô đun và acgumen khác nhau nhau 2kπ (k là số nguyên) được gọi là số phức liên hợp của nhau.
- Argument của số phức z được tính bằng công thức: $$\varphi=arc\tan(\frac ba)$$. Trong đó a và b là phần thực và phần ảo của z.
Mối liên hệ giữa dạng lượng giác và dạng đại số của z
Mọi số phức z ≠ 0 đều có thể biểu diễn dưới dạng lượng giác. Từ dạng đại số z=a+bi (a, b là số thực), ta có thể tìm được mô đun r và acgumen φ bằng công thức: r = căn bậc hai của tổng a bình phương và b bình phương.
$$\varphi=arc\tan(\frac ba)$$
Ngược lại, từ dạng lượng giác của số phức z=r(cosφ+isinφ), ta có thể chuyển về dạng đại số bằng công thức:
a = rcosφ
b = rsinφ
Ngoài dạng lượng giác và dạng đại số thông thường, số phức còn có một dạng nữa đó là dạng mũ. Cho số phức z=a+bi (a, b là số thực) và số mũ thực n, ta có thể định nghĩa dạng mũ của số phức z như sau:
$$z^n=(a+bi)^n$$
Các phép tính với số phức
Để làm tốt những dạng toán liên quan tới dạng lượng giác của số phức, bạn cần nắm vững những công thức tính toán cơ bản như sau:
Công thức chia số phức
Cho hai số phức z1=a1+b1i và z2=a2+b2i (với z2 khác 0), ta có thể chia số phức z1 cho z2 bằng công thức chia số phức như sau:
$$\frac{z1}{z2}=\frac{(a1+b1i)}{(a2+b2i)}=\frac{(a1+b1i)(a2-b2i)}{(a2+b2i)(a2-b2i)}=(a1a2+b1b2)/(a2^2+b2^2)+i(b1a2-a1b2)a2^2+b2^2$$
Ví dụ:
- Chia số phức z1=1+2i cho z2=2−i:
$$\frac{z1}{z2}=\frac{(1+2)}{(2-i)}=\frac{(1+2i)(2+i)}{(2-i)(2+i)}=\frac{(1+4i+2i^2)}{(4+1)}=\frac{-3}5+\frac65i$$
Chú ý:
- Phân số z2 (số phức dùng để chia) không được bằng 0.
- Kết quả của phép chia số phức là một số phức mới.
Cách tính lũy thừa số phức
Công thức:
Cho số phức z=a+bi (a, b là số thực) và số mũ thực n, cách tính lũy thừa số phức bằng phương pháp lượng giác như sau:
- Viết z dưới dạng lượng giác: z=r(cosφ+isinφ) (với r là mô đun và φ là acgumen của z).
- Thay z vào công thức lũy thừa:zn = rn(cos(nφ) + isin(nφ))
Ứng dụng của lượng giác hoá số phức
Việc biểu diễn số phức dưới dạng lượng giác giúp ta dễ dàng thao tác, tính toán và giải quyết các bài toán phức tạp một cách hiệu quả. Dưới đây là một số ứng dụng nổi bật của lượng giác hóa số phức:
Giải phương trình phức
Lượng giác hóa số phức giúp ta dễ dàng giải các phương trình phức, đặc biệt là phương trình bậc hai và bậc cao. Bằng cách biểu diễn các số phức dạng lượng giác, ta có thể chuyển đổi phương trình về dạng lượng giác đơn giản, từ đó tìm được nghiệm bằng các công thức lượng giác quen thuộc.
Tính tích số phức
Phương pháp này còn giúp chúng ta tính tích của nhiều số phức một cách nhanh chóng và hiệu quả. Bằng cách biểu diễn các số phức dạng lượng giác, ta có thể áp dụng các công thức nhân số phức dạng lượng giác để tính tích của chúng.
Ứng dụng trong điện tử
Khi phân tích mạch điện xoay chiều, ta thường sử dụng số phức để biểu diễn điện áp, dòng điện và các đại lượng điện khác. Lượng giác hóa số phức giúp ta dễ dàng thao tác với các đại lượng điện phức này, từ đó tính toán được các thông số quan trọng của mạch điện như công suất, độ lệch pha,…
Lượng giác hóa số phức được sử dụng để tính toán dòng điện, điện áp trong các mạch điện xoay chiều một cách chính xác và hiệu quả.
Ứng dụng trong vật lý
Sóng điện từ được mô tả bằng các phương trình Maxwell, trong đó các đại lượng điện từ như điện trường, từ trường được biểu diễn bằng số phức. Phương pháp lượng giác hóa số phức giúp ta dễ dàng thao tác với các phương trình Maxwell, từ đó tính toán được các đặc điểm của sóng điện từ như bước sóng, tần số,…
Bài tập lượng giác hoá số phức
Dưới đây là một số bài tập về dạng lượng giác của số phức giúp bạn củng cố lý thuyết và luyện tập giải Toán đối với dạng này:
Bài tập 1:

Bài tập 2:

Bài tập 3:

Lời kết
Lượng giác hóa số phức là một công cụ toán học mạnh mẽ với nhiều ứng dụng thực tế trong các lĩnh vực toán học, điện tử, vật lý,… Hiểu rõ sẽ giúp bạn mở rộng kiến thức toán học và giải quyết nhiều bài toán phức tạp một cách hiệu quả.




