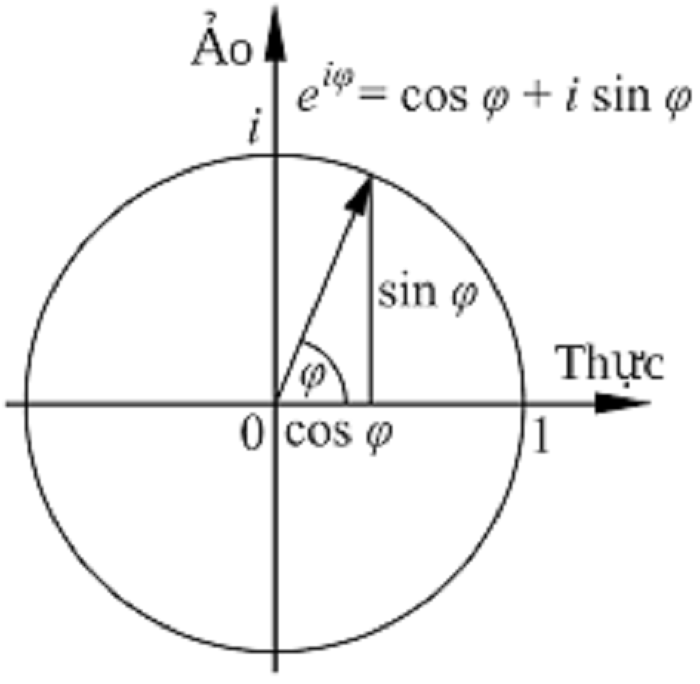
Bảng giá trị lượng giác luôn là một trong những nội dung quan trọng nhất trong chương trình giáo dục toán học. Đây là nội dung được đánh giá là sở hữu lượng kiến thức lớn, dễ gây nhầm lẫn đối với không ít người. Để mọi người có thể tiếp cận kiến thức này dễ hơn, bảng lượng giác đã được ra đời. Bài viết dưới đây, chúng tôi sẽ cung cấp cho bạn đầy đủ các thông tin về nội dung này.
Bảng giá trị lượng giác là gì?
Bảng giá trị lượng giác (bảng lượng giác góc đặc biệt) là một bảng số liệt kê các giá trị của các hàm lượng giác cơ bản như sin, cos, tan, cot, sec, csc tương ứng với các góc đặc biệt thường gặp trong toán học. Bảng này cung cấp một công cụ hữu ích để nhanh chóng tìm giá trị của các hàm lượng giác mà không cần phải tính toán trực tiếp từ các công thức.
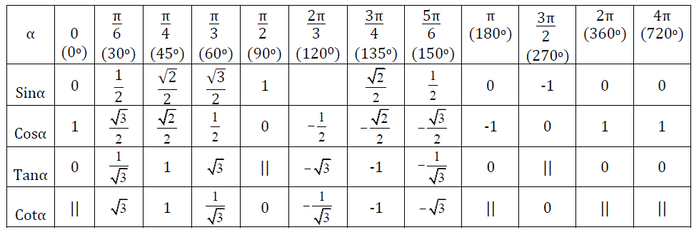
Bảng lượng giác thường bao gồm giá trị lượng giác của các góc đặc biệt như 0°, 30°, 45°, 60°, 90°, và các góc tương ứng trong các góc phần tư khác nhau (từ 0° đến 360°). Đối với mỗi góc đặc biệt, bảng sẽ liệt kê giá trị của các hàm lượng giác sin, cos, tan, cot, sec, csc tương ứng. Các giá trị này được tính toán chính xác đến một số chữ số thập phân nhất định, thường là từ 4 đến 8 chữ số.
Bảng giá trị lượng giác đặc biệt rất hữu ích trong việc giải các bài toán liên quan đến hình học, lượng giác, và nhiều lĩnh vực khác như vật lý, kỹ thuật, thiên văn học. Thay vì phải tính toán trực tiếp từ các công thức lượng giác, chúng ta có thể tra bảng để nhanh chóng tìm được giá trị chính xác của các hàm lượng giác tương ứng với góc cần xét. Điều này giúp tiết kiệm thời gian và giảm nguy cơ sai sót trong các phép tính phức tạp.
Bảng giá trị lượng giác đặc biệt
Dưới đây là bảng thống kê giá trị các góc lượng giác đặc biệt:
| Góc | Sin | Cos | Tan | Cot | Sec | Csc |
| 0° | 0 | 1 | 0 | Không xác định | 1 | Không xác định |
| 30° | 1/2 | √3/2 | 1/ √3 | √3 | 2/ √3 | 2 |
| 45° | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 90° | 1 | 0 | Không xác định | 0 | Không xác định | 1 |
| 120° | √3/2 | -1/2 | -√3 | -1/√3 | 2 | -2/√3 |
| 135° | √2/2 | -√2/2 | -1 | -1 | √2 | -√2 |
| 150° | 1/2 | -√3/2 | -1/√3 | -√3 | 2/√3 | -2 |
| 180° | 0 | -1 | 0 | Không xác định | -1 | Không xác định |
Ứng dụng của bảng giá trị lượng giác
Bảng lượng giác có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau. Dưới đây là một số ứng dụng tiêu biểu:
Đơn giản hóa bài toán
Trong toán học, bảng góc lượng giác được sử dụng rộng rãi để giải các bài toán liên quan đến lượng giác và hình học. Khi cần tính các giá trị của các hàm lượng giác như sin, cos, tan,… tương ứng với một góc nhất định, chúng ta có thể tra cứu bảng để nhanh chóng tìm được kết quả chính xác mà không cần phải tính toán trực tiếp từ công thức. Điều này giúp tiết kiệm thời gian và tránh sai sót trong các phép tính phức tạp.
Tính toán trong vật lý học
Trong lĩnh vực vật lý, bảng lượng giác đóng vai trò quan trọng trong việc tính toán các vectơ lực, chuyển động trong điện từ học, quang học và nhiều lĩnh vực khác. Ví dụ, trong quang học, chúng ta có thể sử dụng bảng để tính toán các hiện tượng phản xạ và khúc xạ ánh sáng dựa trên góc tới và góc khúc xạ.
Tính thông số góc trong xây dựng
Trong ngành kỹ thuật và xây dựng, bảng lượng giác là công cụ không thể thiếu để tính toán các thông số liên quan đến góc nghiêng, góc hợp lực, góc đỉnh trong các kết cấu, cầu đường và các công trình khác. Nó giúp các kỹ sư và kiến trúc sư đảm bảo tính chính xác và an toàn trong thiết kế.
Xác định thông tin chính xác trong hàng hải và hàng không
Ngoài ra, bảng lượng giác đặc biệt cũng có ứng dụng trong lĩnh vực hàng hải và hàng không. Trong những lĩnh vực này, các nhà điều hành phải thường xuyên tính toán các góc liên quan đến hướng đi, góc độ cao, góc lái,… Bảng lượng giác giúp họ nhanh chóng và chính xác xác định các thông số này, đảm bảo an toàn cho các chuyến bay và chuyến đi.
Tóm lại, bảng giá trị lượng giác là một công cụ hữu ích và quan trọng trong nhiều lĩnh vực, giúp các nhà khoa học, kỹ sư và chuyên gia thực hiện các phép tính liên quan đến lượng giác một cách nhanh chóng và chính xác.
Một số câu hỏi thường gặp
Khi tìm hiểu về bảng lượng giác, chúng tôi thường xuyên bắt gặp các thắc mắc sau:
Bảng giá trị lượng giác được học từ năm lớp mấy?
Giá trị lượng giác đã được đưa vào giảng dạy từ năm lớp 9. Tuy nhiên, vào giai đoạn học trung học phổ thông các bạn học sinh mới được tiếp cận với bảng giá trị lượng giác lớp 10.
Các góc đặc biệt trong lượng giác bao gồm những góc nào?
Dưới đây là các góc đặc biệt trong lượng giác:
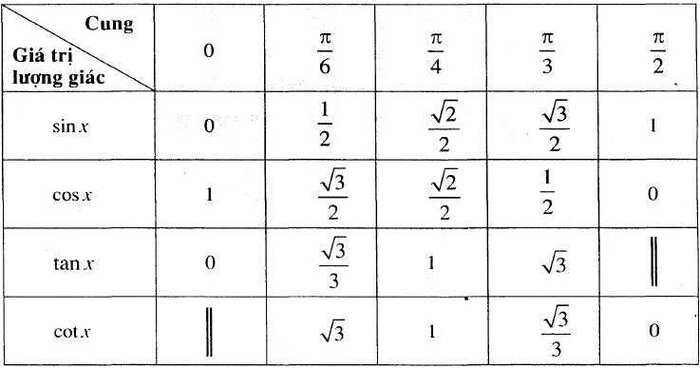
- 0° (không độ) và 360° (hay cũng có thể viết là 0°): Đây là góc đặc biệt quan trọng, tương ứng với một đường thẳng. Với góc 0°, giá trị sin = 0, cos = 1, tan = 0.
- 30°, 60° và 90°: Đây là các góc trong tam giác vuông cơ bản. Góc 30° và 60° là góc nhọn, còn 90° là góc vuông. Các giá trị lượng giác tương ứng của chúng là:
- 30°: sin = 1/2, cos = √3/2, tan = 1/√3
- 60°: sin = √3/2, cos = 1/2, tan = √3
- 90°: sin = 1, cos = 0, tan = không xác định
- 45° và các góc đối xứng 135°, 225°, 315°: Đây là các góc quan trọng, thường gặp trong hình học. Giá trị lượng giác của 45° là sin = cos = √2/2, tan = 1.
- 180° và các góc đối xứng 180° + n × 180°: Đây là các góc phẳng, tương ứng với một đường thẳng đối diện ban đầu. Với góc 180°, giá trị sin = 0, cos = -1, tan = 0.
Lời kết
Có thể thấy, bảng giá trị lượng giác là một công cụ đắc lực và thiết yếu trong lĩnh vực toán học cũng như nhiều lĩnh vực khác liên quan. Chúng tôi hy vọng những thông tin chúng tôi cung cấp phía trên có thể giúp ích cho bạn trong quá trình nghiên cứu và học tập về nội dung này.