Bán kính hình tròn là đại lượng quan trọng, có liên quan đến diện tích, chu vi và đường kính. Do đó chúng ta có thể tính được bán kính nếu biết được giá trị các thuộc tính trên và ngược lại. Đây là kiến thức trọng tâm trong chương trình học nên bạn cần thực hành bài tập nhiều lần.
Bán kính hình tròn là gì?
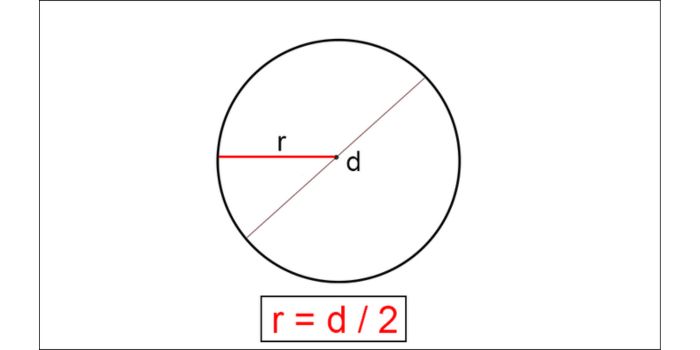
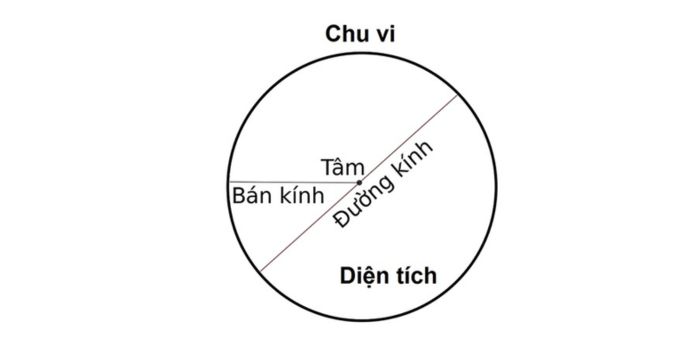
Bán kính hình tròn (bán kính của đường tròn) là khoảng cách tính từ tâm hình tròn đến một điểm bất kỳ trên đường tròn của nó.
Trong toán học, bán kính của hình tròn được ký hiệu bằng chữ “r”. Giá trị của bán kính là không thay đổi trong một hình tròn. Đây là yếu tố quan trọng trong việc tính toán và xác định các thuộc tính của hình tròn đó.
Xem thêm: Khái niệm ht là gì? Tính chất của hình tròn
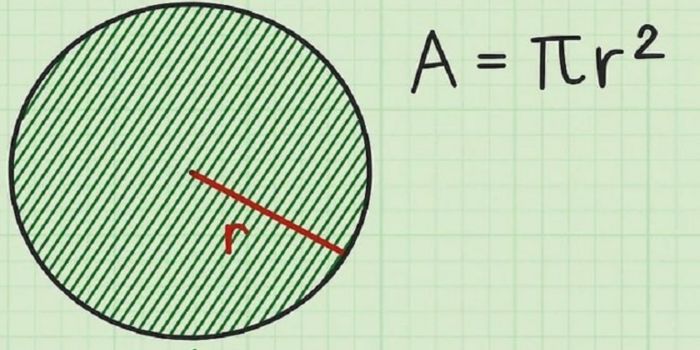
Cách tính bán kính hình tròn
Để tính bán kính của một hình tròn, bạn có thể sử dụng một trong 3 công thức sau đây:
Công thức tính bán kính khi biết đường kính
Đường kính hình tròn là độ dài của một đường thẳng đi qua tâm của hình tròn và nối hai điểm trên đường viền của hình tròn. Để tính bán kính từ đường kính, ta có công thức sau:
$$r=\;\frac D2$$
Trong đó:
- D: Đường kính hình tròn.
- r: Bán kính của hình tròn
Ví dụ: Tính bán kính của một hình tròn có đường kính là 15cm.
Giải: Bán kính (r) = 15 / 2 = 7.5cm
Tìm hiểu thêm: Hình tròn có cạnh không? Đặc điểm của hình tròn
Công thức tính bán kính từ chu vi hình tròn
Chu vi của một hình tròn (C) là độ dài của đường viền hoàn chỉnh của hình tròn đó. Khi biết được chu vi hình tròn, chúng ta có thể xác định được bán hình theo công thức sau:
$$r\;=\;\frac C{2\pi}$$
Trong đó:
- Chu vi (C) là độ dài của đường viền của hình tròn.
- π (pi): hằng số Archimedes có giá trị xấp xỉ 3.14
- r: Bán kính của hình tròn
Ví dụ: Tính bán kính của một hình tròn có chu vi là 15cm
Giải: Bán kính (r) = 15/(2 * 3.14) ≈ 2.38cm
Công thức tính bán kính hình tròn khi biết diện tích
Diện tích của một hình tròn (A) là khu vực bên trong đường viền của hình tròn đó. Khi biết diện tích (A), bạn áp dụng công thức để xác định bán kính như sau:
$$r\;=\;\sqrt{ A\;/\;\pi}$$
Trong đó:
- Diện tích (A) là khu vực bên trong của hình tròn
- π (pi): hằng số Archimedes có giá trị xấp xỉ 3.14
- r: Bán kính của hình tròn
Ví dụ: Tính bán kính của một hình tròn có diện tích là 50.24cm
Giải: Bán kính (r) = √(50.24/π (3.14)) = 4cm
Một số bài toán thực hành tại nhà
Để ghi nhớ và thành thạo kiến thức về cách tính bán hình đường tròn, bạn cần thực hành nhiều bài tập liên quan. Dưới đây là một số bài toán gợi ý dành cho bạn:
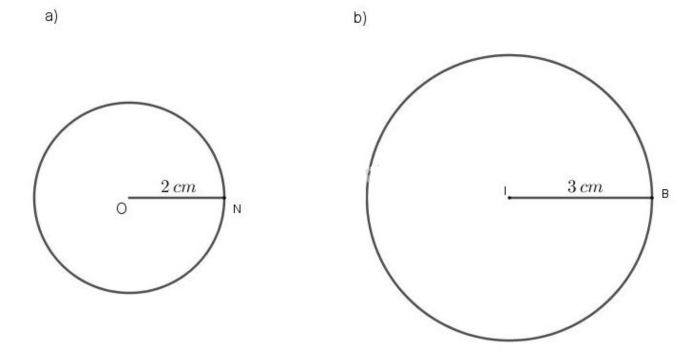
- Bài tập 1: Một hồ nước hình tròn có bán kính là 5m, hãy tính chu vi và diện tích của hồ nước này.
- Bài tập 2: Cho 1 đĩa CD có độ dài đường kính là 12cm. Xác định chu vi và bán kính của CD trên.
- Bài tập 3: Cho biết chu vi của một sân bóng tròn là 66m. Vậy diện tích của sân bóng trên là bao nhiêu?
- Bài tập 4: Một bàn tròn có đường kính 1m. Hãy tính diện tích và chu vi của bàn tròn đó.
- Bài tập 5: Một chiếc bánh pizza hình tròn có chu vi là 20cm. Hãy tính diện tích và bán kính của chiếc bánh trên.
Xem ngay: Công thức tính diện tích hình tròn và bài tập áp dụng
Lưu ý cần biết khi làm bài tập tính bán kính
Tính bán kính hình tròn là bài tập quan trọng khi giải toán hình học. Để đảm bảo áp dụng đúng công thức và ra kết quả chính xác, bạn đừng quên các lưu ý sau:
- Xác định thông tin đã cho: Đọc và hiểu đề bài để xác định thông tin đã cung cấp. Điều này có thể bao gồm đường kính, chu vi, diện tích hoặc các thông tin khác liên quan đến hình tròn.
- Sử dụng công thức chính xác: Dựa vào thông tin đã cho, áp dụng công thức chính xác để tính bán kính. Sử dụng đúng công thức phù hợp với thông tin đã cung cấp (đường kính, chu vi, diện tích).
- Chú ý đơn vị đo: Đảm bảo rằng các đơn vị đo được sử dụng đồng nhất trong bài tập. Bạn nên chuyển đổi đơn vị trước khi tính để đảm bảo tính toán chính xác.
- Làm tròn kết quả: Khi làm tròn kết quả, tuân theo yêu cầu của đề bài hoặc theo quy tắc làm tròn thông thường.
- Kiểm tra lại kết quả: Sau khi tính toán xong, hãy kiểm tra lại kết quả để chắc chắn rằng nó hợp lý và phù hợp với yêu cầu của bài tập.
- Đọc lại đề bài: Trước khi kết thúc, hãy đọc lại đề bài một lần nữa để đảm bảo rằng đã trả lời đúng câu hỏi và đáp ứng đầy đủ yêu cầu của bài tập.
Ứng dụng của bán kính trong thực tế
Bán kính là một khái niệm quan trọng trong hình học và có nhiều ứng dụng thực tế. Dưới đây là một số ví dụ về ứng dụng của bán kính trong cuộc sống hàng ngày:
- Kiến trúc và xây dựng: Bán kính được sử dụng để thiết kế và xác định kích thước của các cấu trúc tròn trong kiến trúc. Chẳng hạn như cột tròn, cầu tròn, hoặc khuôn viên hình tròn của các công trình xây dựng.
- Kỹ thuật đo lường: Bán kính được sử dụng trong các công cụ đo lường để xác định kích thước và độ dài của các vật thể tròn hoặc các đường tròn liên quan.
- Khoa học tự nhiên: Bán kính được sử dụng trong nhiều lĩnh vực của khoa học tự nhiên, chẳng hạn như trong nghiên cứu vật lý, thiên văn học, sinh học,…
Nắm vững lý thuyết và công thức giúp bạn xác định bán kính hình tròn dễ dàng. Đây là một khái niệm cơ bản và có sự hiện diện rộng rãi trong nhiều lĩnh vực khác nhau. Hãy theo dõi trang Học Thế Nào để cùng ôn luyện kiến thức một cách hiệu quả nhất!