Chu vi hình hộp tam giác là gì, cách tính như thế nào, áp dụng được gì trong thực tế? Tất cả đều sẽ được giải đáp trong bài viết dưới đây.
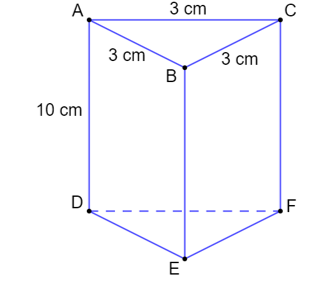
Hình hộp tam giác, còn được gọi là lăng trụ tam giác, là một hình khối được tạo thành bởi hai đáy là hai tam giác bằng nhau và song song với nhau, cùng với ba mặt bên là hình chữ nhật. Đây là một trong những hình dạng hình học cơ bản và quen thuộc trong chương trình toán học từ cấp tiểu học đến cấp trung học cơ sở.
Chu vi hình hộp tam giác là gì? Công thức tính
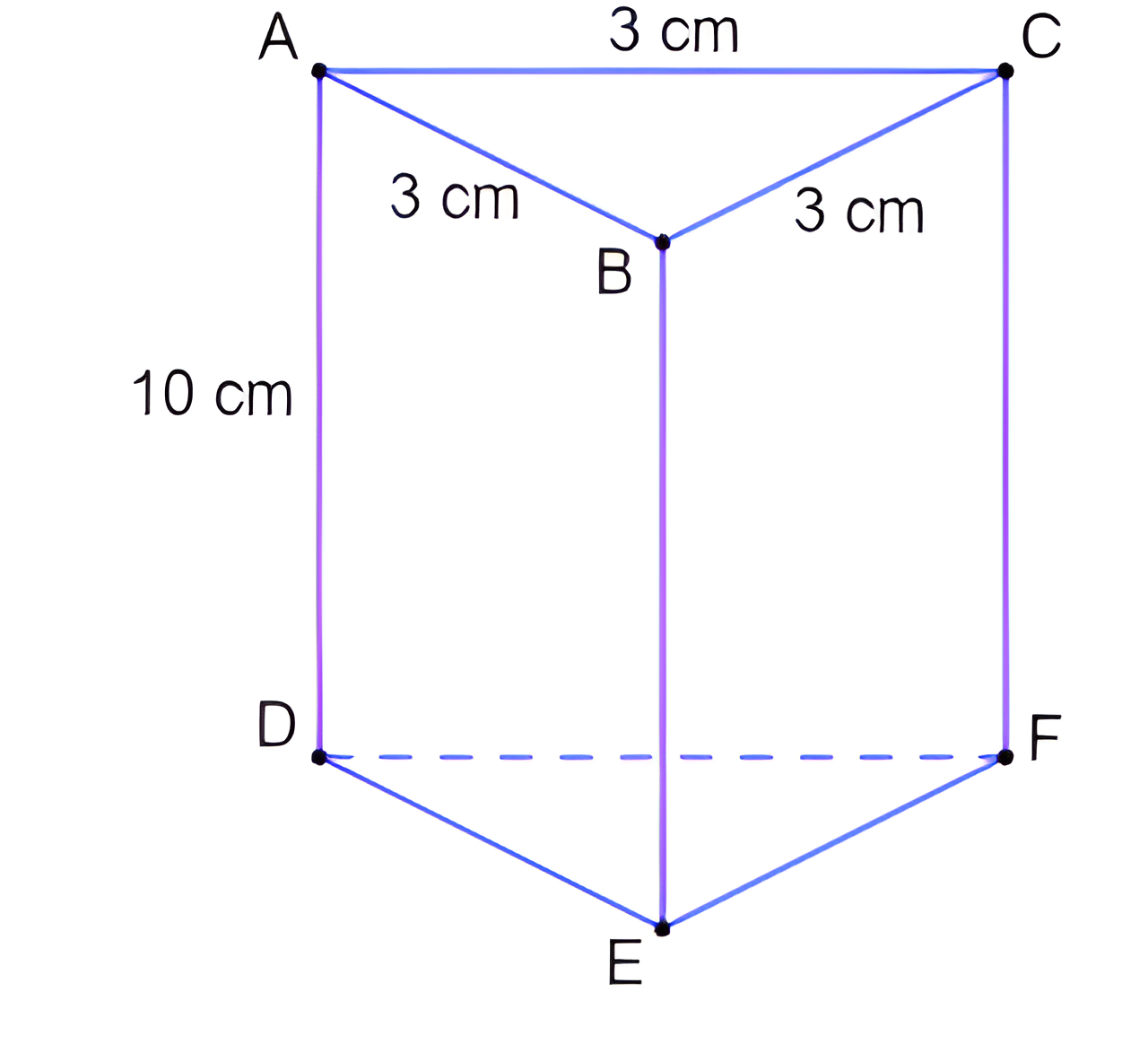
Chu vi của hình hộp tam giác là tổng độ dài của tất cả các cạnh của hình hộp. Đơn giản hơn, đó chính là khoảng cách quanh hình hộp tam giác. Để tính chu vi của hình hộp tam giác, chúng ta cần biết độ dài của các cạnh của nó.
Ký hiệu
Trong công thức tính chu vi hình hộp tam giác, chúng ta sẽ sử dụng các ký hiệu sau:
- Chu vi: P
- Độ dài cạnh đáy: a, b, c
- Độ dài cạnh bên: h
Công thức tổng quát
Công thức tính chu vi hình hộp tam giác có dạng:
$$P=2\times(a+b+c)+3h$$
Các loại chu vi lăng trụ tam giác
Lăng trụ tam giác có thể được phân loại dựa trên hình dạng của đáy và cạnh bên. Dưới đây là những dạng chu vi phổ biến của lăng trụ tam giác.
Lăng trụ tam giác đều
Đây là một trong những dạng chu vi đơn giản nhất của lăng trụ tam giác. Đặc điểm của lăng trụ tam giác đều là:
- Đáy là tam giác đều.
- Cạnh bên vuông góc với đáy.
- Chu vi:
$$P=6a+3h$$
(a là độ dài cạnh đáy, h là độ dài cạnh bên)
Lăng trụ tam giác vuông
Đây là một dạng chu vi phổ biến khác của lăng trụ tam giác. Thay vì có đáy là tam giác đều, lăng trụ tam giác vuông có đáy là tam giác vuông. Điều này ảnh hưởng đến công thức tính chu vi như sau:
- Đáy là tam giác vuông.
- Cạnh bên vuông góc với đáy.
- Chu vi:
$$P=2\times(a+b+c)+3h$$
(a, b, c là độ dài các cạnh đáy, h là độ dài cạnh bên)
Lăng trụ tam giác tù
Trong trường hợp đáy của lăng trụ tam giác là tam giác tù, công thức tính chu vi sẽ có sự khác biệt nhất định. Chúng ta sẽ cần tính toán độ dài của từng cạnh riêng lẻ và cộng lại để có được chu vi cuối cùng.
Cách tính chu vi lăng trụ tam giác
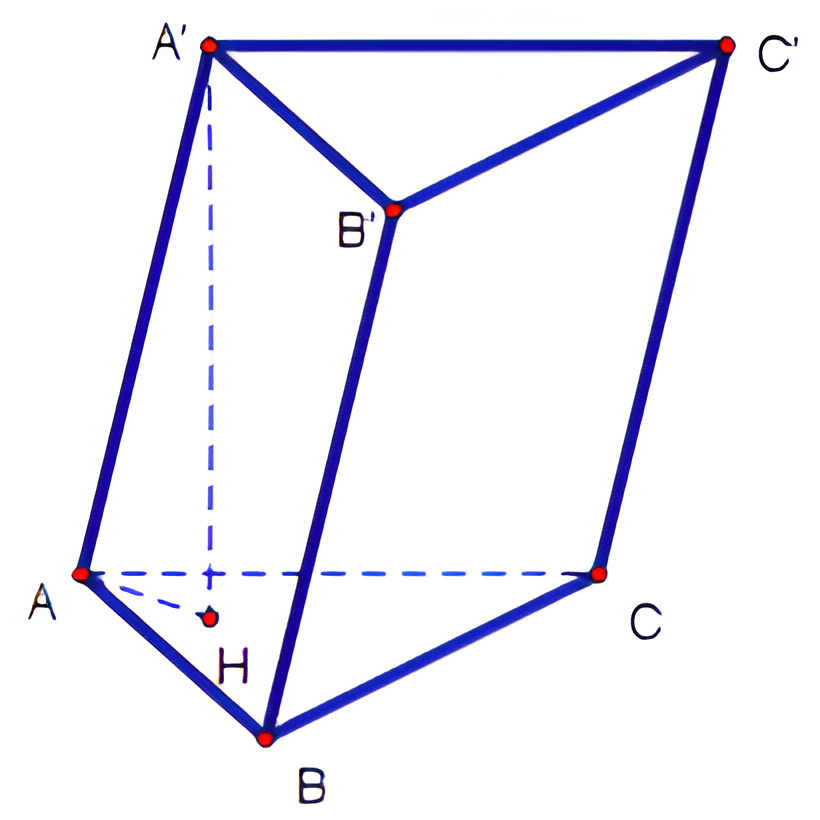
Bây giờ chúng ta đã biết các dạng chu vi phổ biến của lăng trụ tam giác, hãy cùng tìm hiểu cách tính chu vi cho từng dạng một.
Bước 1: Xác định độ dài các cạnh
Đầu tiên, chúng ta cần xác định độ dài của các cạnh của hình hộp tam giác. Trong trường hợp hình hộp tam giác đều, các cạnh đáy và cạnh bên sẽ bằng nhau. Tuy nhiên, trong trường hợp hình hộp tam giác không đều, chúng ta sẽ cần tính toán từng cạnh riêng lẻ.
Bước 2: Áp dụng công thức
Sau khi đã biết độ dài của các cạnh, chúng ta có thể áp dụng công thức tính chu vi để tính toán kết quả cuối cùng. Hãy cùng xem một số ví dụ minh họa để hiểu rõ hơn về cách tính chu vi cho từng dạng lăng trụ tam giác.
Ví dụ minh họa
Ví dụ 1: Lăng trụ tam giác đều
Giả sử chúng ta có một hình hộp tam giác đều có độ dài cạnh đáy là 5cm và độ dài cạnh bên là 3cm. Ta có thể tính chu vi như sau: $$P=6a+3h=6\times5+3\times3=30+9=39(cm)$$
Ví dụ 2: Lăng trụ tam giác vuông
Giả sử chúng ta có một lăng trụ tam giác vuông với đáy là tam giác vuông có cạnh góc vuông là 6cm và cạnh bên là 4cm. Ta có thể tính chu vi như sau: $$P=2\times(a+b+c)+3h=2\times(6+6+6)+3\times4=36+12=48(cm)$$
Ví dụ 3: Lăng trụ tam giác tù
Giả sử chúng ta có một lăng trụ tam giác tù với đáy là tam giác tù có các cạnh lần lượt là 7cm, 8cm và 10cm. Cạnh bên của hình hộp tam giác này có độ dài là 2cm. Ta có thể tính chu vi như sau: $$P=a+b+c+3h=7+8+10+3\times2=25+6=31(cm)$$
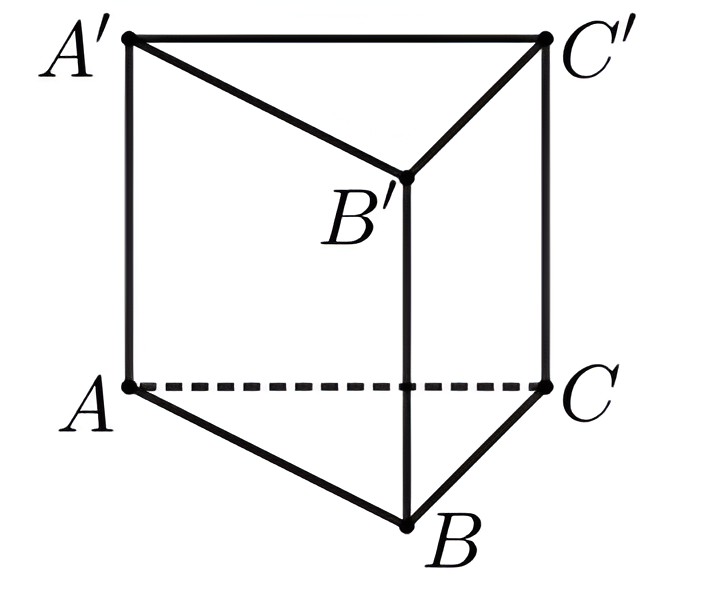
Hình hộp tam giác là hình dạng rất phổ biến trong cuộc sống hàng ngày, được áp dụng trong nhiều lĩnh vực khác nhau, từ kiến trúc đến công nghệ.
Trong toán học, chu vi lăng trụ tam giác được sử dụng để tính toán độ dài các cạnh, từ đó áp dụng công thức để tính diện tích của hình hộp tam giác.
Một ví dụ điển hình là trong kiến trúc, hình hộp tam giác và lăng trụ tam giác được sử dụng để tạo ra các công trình có hình dạng độc đáo và ấn tượng. Các kỹ sư cần phải tính toán chu vi của các hình này để đảm bảo tính chính xác và độ cứng của công trình.
Ngoài ra, chu vi khối hộp tam giác và lăng trụ tam giác cũng được áp dụng trong công nghệ, đặc biệt là trong thiết kế máy móc và các bản vẽ kỹ thuật. Khi tính toán các kích thước cho một chi tiết máy hoặc bản vẽ, các kỹ sư cần phải tính toán chu vi của các hình hộp tam giác và lăng trụ tam giác liên quan đến chi tiết đó.
Bài tập thực hành
Để rèn luyện kỹ năng tính chu vi khối hộp tam giác và lăng trụ tam giác, chúng ta có thể thực hiện các bài tập sau:
Bài Tập 1: Tính chu vi của lăng trụ tam giác đều có cạnh đáy là 4cm và cạnh bên là 2cm.
Bài Tập 2: Tính chu vi của lăng trụ tam giác vuông có cạnh góc vuông là 8cm và cạnh bên là 5cm.
Bài Tập 3: Tính chu vi của lăng trụ tam giác tù có các cạnh lần lượt là 6cm, 9cm và 12cm. Cạnh bên của hình hộp tam giác này có độ dài là 3cm.
Kết luận
Chu vi hình hộp tam giác là một khái niệm quan trọng trong hình học và toán học. Để tính toán chu vi của hình hộp tam giác, chúng ta cần biết công thức tính và áp dụng cho từng dạng cụ thể. Việc rèn luyện kỹ năng tính chu vi sẽ giúp chúng ta hiểu rõ hơn về những khái niệm cơ bản này và áp dụng vào cuộc sống hàng ngày.