Chứng minh hình thang cân là một kỹ năng quan trọng trong hình học, giúp chúng ta hiểu rõ hơn về các tính chất đặc biệt của loại hình này. Để biết được các cách chứng minh, mời các bạn cùng theo dõi một số phương pháp và bài tập vận dụng ngay trong bài viết dưới đây!
Các dấu hiệu nhận biết hình thang cân
Có 2 dấu hiệu để nhận nhận biết hình thang cân:
- Nếu trong hình thang hai góc kề một đáy bằng nhau, thì đây là hình thang cân.
- Nếu hai đường chéo của hình thang bằng nhau, thì đây cũng là hình thang cân.
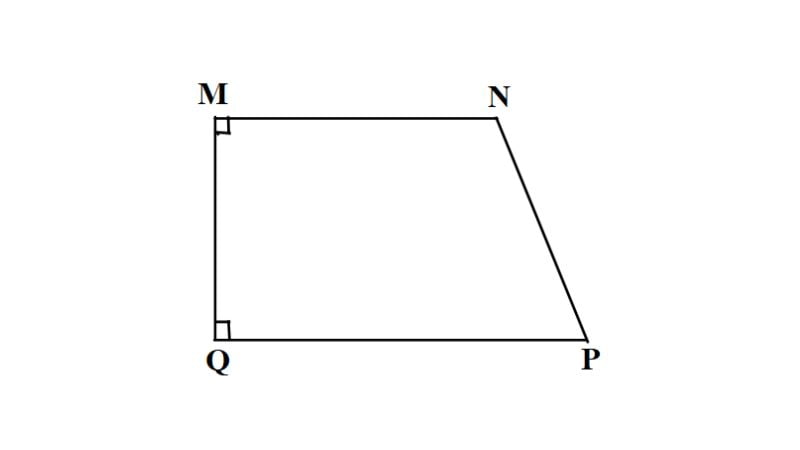
Lưu ý: Hình thang cân có hai cạnh bên bằng nhau, nhưng nếu một hình thang chỉ có hai cạnh bên bằng nhau thì chưa chắc đó là hình thang cân. Ví dụ có thể thấy trong hình vẽ dưới đây:
Đọc ngay: Hình thang cân là gì? Tính chất, đặc điểm như thế nào?
Cách chứng minh hình thang cân chính xác
Hiện tại có ba cách chứng minh hình thang cân chính. Tùy vào dữ liệu và yêu cầu của bài toán, bạn có thể áp dụng một trong ba phương pháp sau:
Phương pháp 1: Chứng minh hai góc kề một cạnh đáy bằng nhau
Phương pháp:
Bước 1: Xác định các góc kề một cạnh đáy: Nhớ lại rằng trong hình thang, hai góc tạo bởi một cạnh đáy với hai cạnh bên được gọi là hai góc kề một cạnh đáy.
Bước 2: Chứng minh hai góc kề một cạnh đáy bằng nhau: Áp dụng 1 trong 3 cách sau:
- Cách 1: Sử dụng tính chất của đường trung bình trong hình thang: Nếu một đường thẳng đi qua trung điểm của một cạnh bên và song song với hai cạnh đáy, nó cũng sẽ đi qua trung điểm của cạnh bên còn lại. Từ đó suy ra hai góc kề cạnh đáy bằng nhau do đối xứng qua trục đường trung bình.
- Cách 2: Sử dụng định lý Thales: Nếu có thể chứng minh được rằng hai cạnh đối của hình thang song song, thì hai góc kề một đáy sẽ bằng nhau do cùng bù với hai góc ở đáy kia của hình thang.
- Cách 3: Áp dụng các tính chất đường phân giác của tam giác: Nếu có thể chứng minh được rằng đường phân giác của một góc ở đáy đi qua trung điểm của cạnh đối diện, ta suy ra hai góc kề đó bằng nhau, vì đường phân giác tạo thành hai tam giác cân.
Bước 3: Suy ra hình thang cân: Sau khi chứng minh được hai góc kề một cạnh đáy bằng nhau, ta có thể suy ra hình thang đó là hình thang cân dựa vào định nghĩa: Hình thang có hai góc kề một cạnh đáy bằng nhau gọi là hình thang cân.
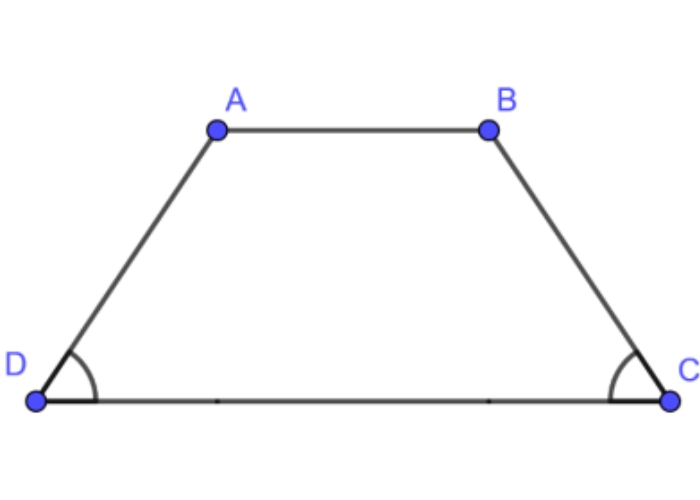
Ví dụ:
Cho hình thang ABCD (AB // CD) có ∠A = ∠C. Chứng minh ABCD là hình thang cân.
Giải
Xác định các góc kề một cạnh đáy:
Góc A và góc C là hai góc kề cạnh đáy CD.
Chứng minh hai góc kề một cạnh đáy bằng nhau:
Ta có ∠A = ∠C (đề bài).
Suy ra hình thang cân:
Theo định nghĩa, hình thang có hai góc kề một cạnh đáy bằng nhau gọi là hình thang cân. Do đó, ABCD là hình thang cân.
Xem ngay: Tổng hợp các dấu hiệu nhận biết hình thang cân đầy đủ, chi tiết nhất
Phương pháp 2: Chứng minh hai đường chéo bằng nhau
Phương pháp:
Để chứng minh hai đường chéo của hình thang cân bằng nhau, bạn có thể áp dụng phương pháp sử dụng các tam giác đồng dạng bên trong hình thang. Dưới đây là các bước chi tiết:
Bước 1: Xác định và vẽ hình: Vẽ hình thang cân ABCD, trong đó AB, CD là hai đáy, AC, BD là hai đường chéo.
Bước 2: Chứng minh các tam giác đồng dạng:
- Chứng minh tam giác ABD đồng dạng với tam giác CDB bằng cách sử dụng định lý về các góc.
- Vì AB song song với CD, góc ABD bằng góc CDB do hai góc này là góc so le trong.
- Sử dụng tính chất tam giác đồng dạng: Khi tam giác ABD đồng dạng với tam giác CDB, theo tính chất của tam giác đồng dạng, ta có AC/BD = AD/BC.
Bước 3: Áp dụng giả thiết hai đường chéo bằng nhau:
- Do giả thiết BD = AC, suy ra BC = AD.
- Kết luận: Vì AD = BC và các tam giác đồng dạng, hai đường chéo AC, BD bằng nhau, chứng tỏ hình thang là cân.
Ví dụ:
Cho hình thang ABCD (AB // CD) có hai đường chéo AC và BD bằng nhau. Chứng minh ABCD là hình thang cân.
Giải
Vẽ hình thang ABCD với hai đường chéo AC và BD cắt nhau tại E.
Kẻ đường trung tuyến ME của tam giác ABD.
Ta có ME là đường trung tuyến của tam giác ABD nên: AE = EB.
Xét hai tam giác ABE và CBE:
- AB chung.
- AE = EB (đã chứng minh).
- BE chung.
Vậy tam giác ABE ~ tam giác CBE (c.c.c).
Suy ra: góc BAE = góc CBE (cặp góc tương ứng).
Ta lại có: Góc BAE và góc CBE là hai góc kề một đáy của hình thang ABCD.
Do đó, ∠BAD = ∠BCD (1).
Xét hai tam giác ACD và BCD:
- CD chung.
- AC = BD (đề bài).
- AD = BC (đã chứng minh ở (1)).
Vậy tam giác ACD ~ tam giác BCD (c.c.c).
Suy ra: góc CAD = góc CBD (cặp góc tương ứng).
Ta lại có: Góc CAD và góc CBD là hai góc kề một đáy của hình thang ABCD.
Do đó, ∠ADC = ∠BCD (2).
Từ (1) và (2), suy ra: ∠BAD = ∠ADC, ∠BCD = ∠BCD.
Vậy ABCD là hình thang cân (định nghĩa).
Phương pháp 3: Sử dụng tính chất hình thang nội tiếp đường tròn
Phương pháp:
- Bước 1: Vẽ đường tròn ngoại tiếp: Vẽ đường tròn đi qua tất cả các đỉnh của hình thang.
- Bước 2: Chứng minh các góc bằng nhau: Sử dụng tính chất hai góc nội tiếp cùng chắn một cung để chứng minh các góc kề một đáy hoặc các góc tạo bởi một cạnh đáy và một đường chéo bằng nhau.
- Bước 3: Suy ra hình thang cân: Dựa vào định nghĩa hoặc các dấu hiệu nhận biết hình thang cân để kết luận.
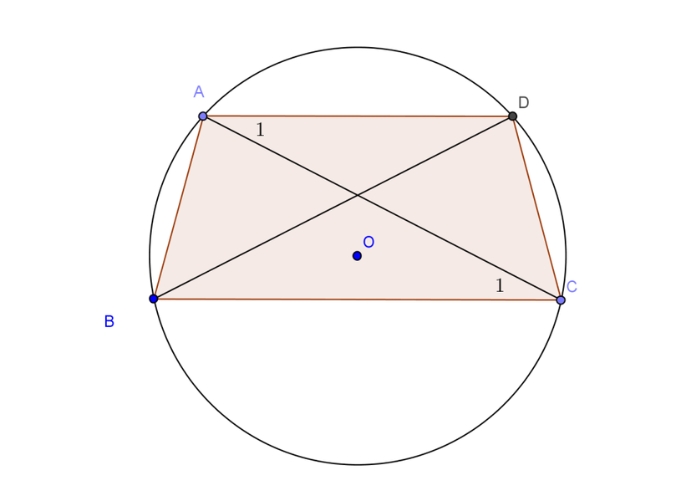
Ví dụ:
Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O). Chứng minh ABCD là hình thang cân.
Giải
Vẽ đường tròn (O) đi qua các điểm A, B, C, D.
Ta có:
- ∠BAD và ∠BCD là hai góc nội tiếp cùng chắn cung BD.
- ∠ADC và ∠ABC là hai góc nội tiếp cùng chắn cung AC.
Theo tính chất hai góc nội tiếp cùng chắn một cung:
- ∠BAD = ∠BCD (1)
- ∠ADC = ∠ABC (2)
Xét hai tam giác ABD và CBD:
- AB = CD (do AB // CD).
- ∠BAD = ∠BCD (đã chứng minh ở (1)).
Góc ABD và góc CBD chung.
Vậy tam giác ABD ~ tam giác CBD (g.c.g).
Suy ra: AD = BC (cặp cạnh tương ứng).
Do đó, ABCD là hình thang cân (định nghĩa).
Tham khảo ngay: Trục đối xứng của hình thang cân là gì? Hình thang cân có mấy trục đối xứng?
Một số bài tập ứng dụng chứng minh hình thang cân
1. Chứng minh bằng hai góc kề một đáy
Bài 1: Cho hình thang ABCD (AB // CD). Biết góc A = 60 độ, góc C = 80 độ. Chứng minh ABCD là hình thang cân.
Giải
Ta có:
- Góc A và góc C kề đáy CD.
- Góc A + góc C = 60 độ + 80 độ = 140 độ.
Vì hai góc kề một đáy có tổng bằng 180 độ nên góc B + góc D = 180 độ – 140 độ = 40 độ.
Mà góc B và góc D cũng là hai góc kề một đáy.
Suy ra: góc B = góc D = 40 độ / 2 = 20 độ.
Xét hai tam giác ABD và CBD:
- AB = CD (do AB // CD).
- Góc A = góc C (đã chứng minh).
- Góc B = góc D (đã chứng minh).
Vậy tam giác ABD ~ tam giác CBD (g.c.g).
Suy ra: AD = BC (cặp cạnh tương ứng).
Do đó, ABCD là hình thang cân (định nghĩa).
Bài 2: Cho hình thang ABCD (AB // CD), biết AD = BC. Chứng minh ABCD là hình thang cân.
Giải
Xét hai tam giác ABD và CBD:
- AB = CD (do AB // CD).
- AD = BC (đề bài).
- AB chung.
Vậy tam giác ABD ~ tam giác CBD (c.c.c).
Suy ra: góc A = góc C (cặp góc tương ứng).
Do đó, ABCD là hình thang cân (định nghĩa).
2. Chứng minh bằng hai đường chéo
Bài 3: Cho hình thang ABCD (AB // CD), biết AC = BD. Chứng minh ABCD là hình thang cân.
Giải
Kẻ đường trung tuyến ME của tam giác ABD.
Ta có:
- E là trung điểm của AD.
- ME // AB (tính chất đường trung tuyến).
Xét hai tam giác AME và BME:
- AM = BM (do E là trung điểm của AD).
- ME chung.
Góc AME = góc BME (hai góc so le trong, AB // ME).
Vậy tam giác AME ~ tam giác BME (g.c.g).
Suy ra: AE = BE (cặp cạnh tương ứng).
Xét hai tam giác AEC và BEC:
- AE = BE (đã chứng minh).
- EC chung.
- Góc AEC = góc BEC (hai góc so le trong, AC // BE).
Vậy tam giác AEC ~ tam giác BEC (g.c.g).
Suy ra: AC = BC (cặp cạnh tương ứng).
Do đó, ABCD là hình thang cân (định nghĩa).
Bài 4: Cho hình thang ABCD (AB // CD), biết hai đường chéo AC và BD cắt nhau tại E. Chứng minh EA = EB.
Giải
Xét hai tam giác ABE và CDE:
- Góc ABE = góc CDE (hai góc đối đỉnh).
- Góc BAE = góc CED (hai góc so le trong, AB // CD).
Ta có:
- AB + BE = AE.
- CD + DE = CE.
Suy ra: AB + CD = AE + CE.
Mà AC = AE + CE (định nghĩa đường chéo).
Vậy AB + CD = AC.
Do đó, EA = EB (đpcm).
Xem thêm: Tính chất hai đường chéo hình thang cân
Ứng dụng của hình thang cân trong thực tiễn và toán học
Hình thang cân có nhiều ứng dụng trong thực tiễn và toán học:
- Đồ chơi trẻ em: Hình thang cân được sử dụng để thiết kế các khối hình học trong bộ xếp hình và đồ chơi giáo dục, giúp trẻ em làm quen với các khái niệm hình học cơ bản.
- Thiết kế nội thất: Hình thang cân thường được áp dụng trong thiết kế bàn, ghế, kệ sách,… nhờ vào tính thẩm mỹ và ổn định của nó.
- Kiến trúc và xây dựng: Các cấu trúc hình thang cân xuất hiện trong kiến trúc như các mái nhà, cầu thang, và các yếu tố trang trí, giúp cân bằng cũng như gia tăng tính đối xứng của công trình.
- Công nghệ: Trong các thiết bị điện tử, hình thang cân được sử dụng trong thiết kế bảng mạch và các chi tiết máy nhờ vào khả năng phân bố lực đều.
- Giải toán hình học: Hình thang cân là đối tượng quan trọng trong các bài toán hình học, từ việc tính diện tích, chu vi, đến chứng minh các tính chất đặc biệt của nó.
- Phát triển kỹ năng tư duy: Các bài toán liên quan đến hình thang cân giúp học sinh phát triển kỹ năng tư duy logic và khả năng giải quyết vấn đề.

Trên đây là hướng dẫn chi tiết các cách chứng minh hình thang cân. Thông qua các bài tập mẫu, Học Thế Nào hy vọng đã giúp bạn hiểu rõ hơn về dạng bài tập này. Nếu vẫn còn thắc mắc, hãy để lại bình luận bên dưới bài viết để được chúng tôi giải đáp cụ thể, chi tiết hơn nhé!