Tìm hiểu diện tích hình chóp cụt: công thức, tính toán và ứng dụng thực tế

Diện tích hình chóp cụt là một trong những khái niệm quan trọng trong hình học không gian. Bài viết này sẽ cung cấp công thức, cách tính và ứng dụng thực tế của diện tích hình chóp cụt trong toán học. Hãy cùng khám phá để hiểu rõ hơn về các thành phần và phương pháp tính toán liên quan.

Diện tích hình chóp cụt và các thành phần cơ bản trong hình học không gian

Hình chóp cụt là gì là một khối đa diện được tạo thành khi cắt một hình chóp bởi một mặt phẳng song song với đáy và không đi qua đỉnh. Khối hình này có hai mặt đáy song song và các mặt bên là hình thang.

Diện tích hình chóp cụt được tính bằng tổng diện tích của hai mặt đáy và diện tích các mặt bên. Công thức tính diện tích toàn phần sẽ là S = S1 + S2 + Sb, trong đó S1, S2 là diện tích hai mặt đáy và Sb là tổng diện tích các mặt bên. Việc nắm vững cách tính này rất quan trọng trong hình học không gian toán.

Đặc điểm hình chóp cụt thể hiện qua cấu trúc độc đáo của nó. Hai mặt đáy song song có hình dạng giống nhau nhưng kích thước khác nhau, với mặt đáy trên luôn nhỏ hơn mặt đáy dưới. Các cạnh bên không song song với nhau mà tạo thành các đường xiên, và nếu kéo dài sẽ gặp nhau tại một điểm chính là đỉnh của hình chóp ban đầu.

Trong thực tế, hình chóp cụt xuất hiện phổ biến trong kiến trúc và xây dựng. Ví dụ như phần thân của tháp Eiffel ở Paris được thiết kế dựa trên nguyên lý của hình chóp cụt, giúp công trình vừa có tính thẩm mỹ vừa đảm bảo độ vững chắc cần thiết.

Công thức tính diện tích xung quanh và diện tích đáy của hình chóp cụt

Để tính toán chính xác diện tích hình chóp cụt, cần xác định được diện tích xung quanh và diện tích hai đáy. Các công thức này giúp giải quyết nhiều bài toán thực tế trong kiến trúc và xây dựng, từ thiết kế mái nhà đến các công trình có hình dạng chóp cụt.

Việc tính toán diện tích của hình chóp cụt đòi hỏi sự kết hợp giữa diện tích xung quanh và diện tích đáy. Trong đó, diện tích xung quanh được tính bằng tổng diện tích các mặt bên, còn diện tích đáy bao gồm diện tích của hai mặt đáy song song.

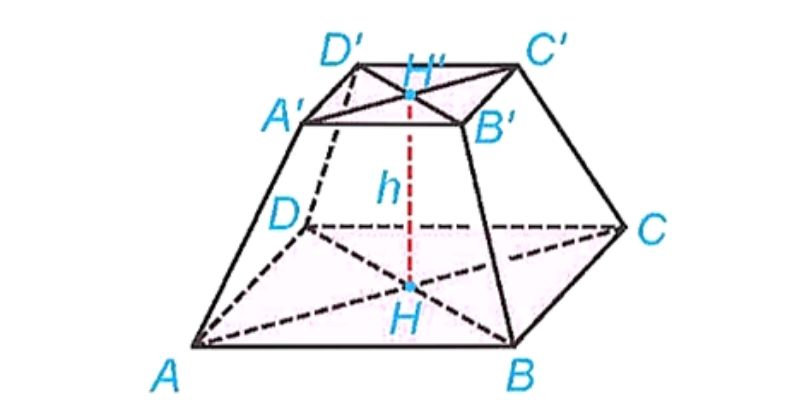
Diện tích xung quanh hình chóp cụt và cách tính

Diện tích xung quanh hình chóp cụt được xác định bằng tổng diện tích các mặt bên hình thang. Mỗi mặt bên là một hình thang với đường cao là độ cao mặt bên và hai đáy song song là các cạnh tương ứng của hai đáy.

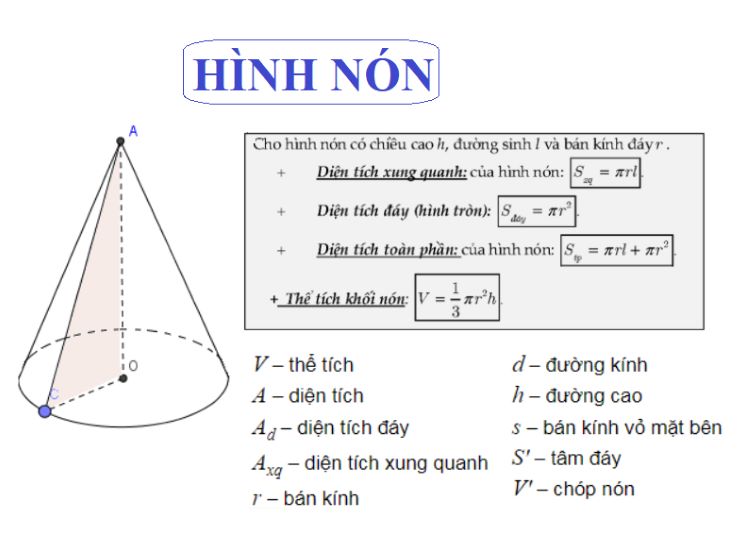
Trong trường hợp hình chóp cụt có đáy là hình tròn, diện tích xung quanh sẽ là một diện tích hình quạt tròn đặc biệt. Công thức tính sẽ là π(R + r)l, với R là bán kính đáy lớn, r là bán kính đáy nhỏ và l là độ dài đường sinh.

Diện tích đáy hình chóp cụt và phương pháp xác định

Diện tích đáy hình chóp cụt là tổng diện tích của hai mặt đáy song song. Tùy thuộc vào hình dạng của đáy, có thể áp dụng các công thức tính diện tích khác nhau. Ví dụ với đáy là hình thoi, có thể sử dụng công thức diện tích hình thoi.

Khi tính toán diện tích đáy, cần chú ý đến tỷ lệ giữa hai đáy song song. Đối với hình chóp cụt đều, tỷ lệ này sẽ giúp xác định mối quan hệ giữa các kích thước của hai đáy, từ đó tính toán chính xác diện tích của từng đáy.

Phương pháp tính diện tích toàn phần hình chóp cụt

Diện tích toàn phần hình chóp cụt được tính bằng tổng của diện tích hai đáy và diện tích các mặt bên. Công thức này áp dụng cho mọi dạng hình chóp cụt, từ hình chóp cụt có đáy là tam giác, tứ giác đến đa giác đều.

Để tính chính xác diện tích hình chóp cụt, cần xác định rõ kích thước của hai đáy và chiều cao của hình chóp cụt. Việc tính toán diện tích mặt bên đòi hỏi phải áp dụng định lý Pythagoras và các công thức lượng giác cơ bản, tương tự như cách tính diện tích khối cầu.

Các bước tính diện tích toàn phần

Bước 1: Xác định diện tích đáy lớn (S1) và diện tích đáy nhỏ (S2) dựa vào hình dạng của đáy.

Bước 2: Tính độ dài cạnh bên của hình chóp cụt bằng công thức l = √(h² + (R-r)²), trong đó h là chiều cao và R, r lần lượt là bán kính đáy lớn, đáy nhỏ.

Bước 3: Tính diện tích mặt bên bằng công thức Sb = (P1 + P2)l/2, với P1, P2 là chu vi đáy lớn và đáy nhỏ.

Bước 4: Tổng hợp công thức diện tích hình chóp cụt toàn phần: S = S1 + S2 + Sb

Ví dụ minh họa chi tiết

Cho hình chóp cụt có đáy là hình vuông, cạnh đáy lớn a = 8cm, cạnh đáy nhỏ b = 4cm, chiều cao h = 6cm.

Diện tích đáy lớn: S1 = a² = 64cm²
Diện tích đáy nhỏ: S2 = b² = 16cm²

Độ dài cạnh bên: l = √(6² + (4-2)²) = √40 ≈ 6.32cm

Diện tích mặt bên: Sb = (32 + 16) × 6.32/2 = 151.68cm²

Vậy diện tích toàn phần = 64 + 16 + 151.68 = 231.68cm²

Hướng dẫn giải các bài toán về diện tích hình chóp cụt

Để tính diện tích hình chóp cụt, ta cần xác định diện tích xung quanh và diện tích hai đáy. Diện tích toàn phần của hình chóp cụt bằng tổng diện tích xung quanh và diện tích hai đáy. Việc tính toán cần dựa trên các yếu tố như chiều cao, cạnh bên, góc nghiêng và kích thước hai đáy.

Khi giải các bài toán về thể tích hình chóp và thể tích hình chóp cụt, ta thường kết hợp với cách tính diện tích hình chóp cụt để giải quyết các bài toán phức tạp hơn. Việc nắm vững công thức và phương pháp tính diện tích sẽ giúp giải quyết hiệu quả nhiều dạng bài tập khác nhau.

Phân tích và lập phương án giải

Bước đầu tiên khi giải bài toán về diện tích hình chóp cụt là phân tích kỹ dữ kiện đề bài. Cần xác định rõ loại hình chóp cụt (tam giác, tứ giác hay đa giác đều), các kích thước đã cho và yêu cầu cần tìm.

Tiếp theo, ta vẽ hình phụ để thấy rõ mối quan hệ giữa các yếu tố. Việc vẽ hình vuông góc, hình chiếu và thiết diện sẽ giúp nhận diện các tam giác đồng dạng, từ đó tìm ra các tỷ số tương ứng.

Cuối cùng là lập phương án giải theo trình tự logic: tính các yếu tố trung gian cần thiết, áp dụng công thức phù hợp và kiểm tra kết quả có hợp lý không.

Các dạng bài tập thường gặp

Dạng 1: Tính diện tích xung quanh khi biết kích thước hai đáy và chiều cao. Với dạng này, ta cần tính độ dài đường sinh và áp dụng công thức diện tích hình thang nhân với số mặt bên.

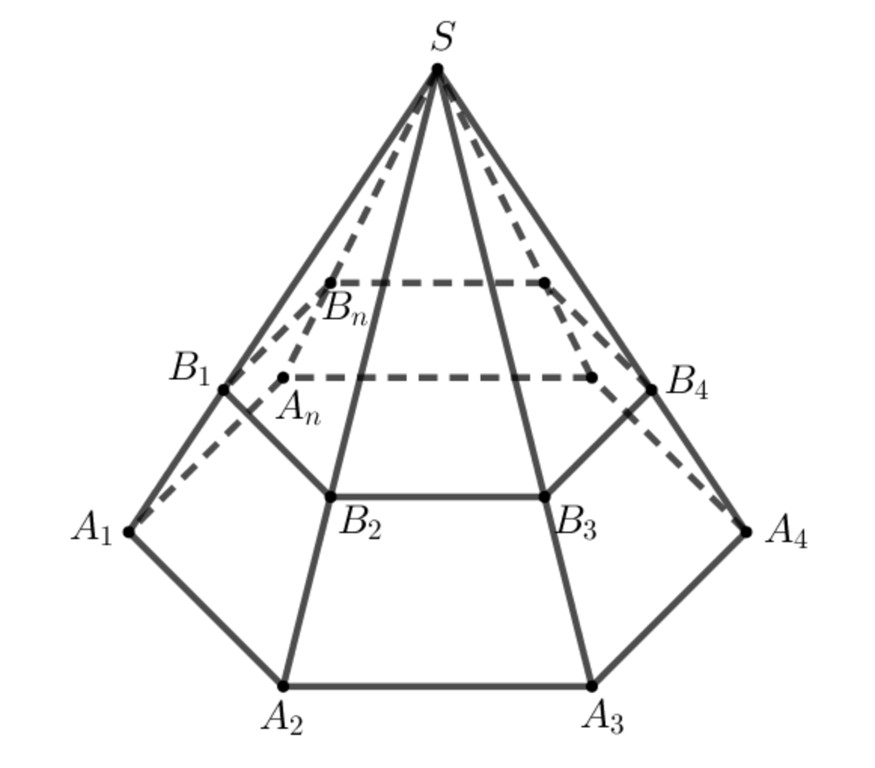
Dạng 2: Tính diện tích toàn phần khi biết góc nghiêng và một số kích thước. Ở đây cần vận dụng kiến thức về tam giác vuông để tìm các yếu tố chưa biết.

Một ví dụ tính diện tích chóp cụt điển hình là bài toán tính diện tích vỏ phễu đổ nước hình chóp cụt có đáy lớn 30cm, đáy nhỏ 10cm và chiều cao 40cm. Việc giải bài toán này đòi hỏi phải tính cả diện tích xung quanh và diện tích hai đáy tròn.

Ứng dụng thực tiễn của diện tích hình chóp cụt trong đời sống và kỹ thuật

Diện tích hình chóp cụt là một công cụ toán học quan trọng được ứng dụng rộng rãi trong nhiều lĩnh vực. Việc tính toán chính xác diện tích của các cấu trúc hình chóp cụt giúp tối ưu hóa việc thiết kế và thi công trong thực tế. Theo Học Thế Nào, ứng dụng diện tích hình chóp cụt có vai trò then chốt trong việc đảm bảo tính chính xác và hiệu quả của nhiều công trình.

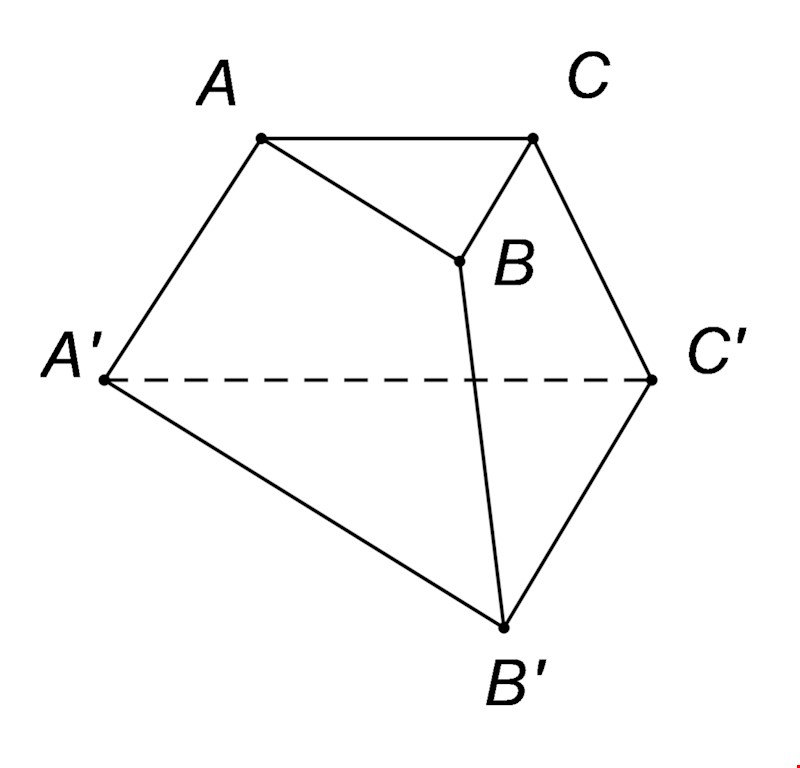
Ứng dụng trong kiến trúc và xây dựng

Trong lĩnh vực kiến trúc, các cấu trúc hình chóp cụt thường xuất hiện ở mái nhà, tháp chuông và các công trình tôn giáo. Theo kiến trúc sư Frank Gehry, việc tính toán chính xác diện tích bề mặt giúp xác định lượng vật liệu cần thiết và chi phí thi công.

Các công trình hiện đại như tòa nhà Burj Al Arab tại Dubai sử dụng hình dạng chóp cụt để tạo nên vẻ đẹp độc đáo và tối ưu khả năng chống gió. Kiến trúc sư Tom Wright đã áp dụng nguyên lý này để thiết kế tòa nhà biểu tượng có hình dáng cánh buồm nổi tiếng.

Trong xây dựng cầu đường, các trụ cầu thường được thiết kế dạng chóp cụt để tăng độ vững chắc và khả năng chịu lực. Ứng dụng chóp cụt trong toán học đã giúp các kỹ sư tính toán chính xác lượng bê tông cần thiết, đảm bảo tính kinh tế và an toàn cho công trình.

Ứng dụng trong công nghiệp và sản xuất

Trong ngành công nghiệp đúc kim loại, các khuôn đúc thường có dạng hình chóp cụt để dễ dàng tháo lắp sản phẩm. Công ty Toyota đã áp dụng nguyên lý này trong thiết kế khuôn đúc các chi tiết ô tô, giúp tăng năng suất sản xuất lên 15%.

Các ống khói nhà máy thường được thiết kế dạng hình chóp cụt để tối ưu luồng khí thải và độ bền công trình. Nghiên cứu của Viện Công nghệ Massachusetts (MIT) chỉ ra rằng thiết kế này giúp giảm 30% sức cản không khí so với ống khói hình trụ thông thường.

Trong sản xuất bao bì, các hộp giấy dạng chóp cụt được sử dụng phổ biến do khả năng xếp chồng tốt và tiết kiệm không gian. Thiết kế này còn giúp tối ưu chi phí vận chuyển và lưu kho, đồng thời tăng tính thẩm mỹ cho sản phẩm.

Diện tích hình chóp cụt là một khái niệm quan trọng trong hình học không gian, đóng vai trò trong nhiều lĩnh vực của đời sống. Bài viết đã phân tích công thức tính diện tích xung quanh, diện tích đáy và diện tích toàn phần của hình chóp cụt, cũng như đưa ra hướng dẫn cụ thể để giải quyết các bài toán liên quan. Với kiến thức này, bạn hoàn toàn có thể áp dụng vào các bài toán thực tiễn và rèn luyện kỹ năng toán học hiệu quả.