Góc giữa 2 mặt phẳng và các phương pháp tính toán hiệu quả trong hình học không gian

Góc giữa 2 mặt phẳng là một khái niệm quan trọng trong hình học không gian. Để hiểu rõ hơn về cách xác định và tính toán góc giữa hai mặt phẳng, hãy cùng khám phá các phương pháp, công thức và bài toán thường gặp. Những kiến thức này sẽ giúp bạn củng cố kỹ năng giải toán hiệu quả và tự tin hơn trong học tập.

Góc giữa 2 mặt phẳng là gì và các khái niệm cơ bản trong hình học không gian

Trong Hình học không gian, góc giữa hai mặt phẳng được định nghĩa là góc nhọn tạo bởi hai đường thẳng vuông góc với đường giao của hai mặt phẳng, mỗi đường thẳng nằm trên một mặt phẳng. Đây là một khái niệm quan trọng giúp xác định vị trí tương đối giữa các mặt phẳng trong không gian ba chiều.

Khi hai mặt phẳng cắt nhau, chúng sẽ tạo thành một đường thẳng gọi là giao tuyến. Tại mỗi điểm trên giao tuyến, ta có thể vẽ hai đường thẳng vuông góc với giao tuyến, mỗi đường nằm trên một mặt phẳng. Góc giữa 2 mặt phẳng chính là góc nhọn tạo bởi hai đường thẳng này.

Để xác định góc giữa hai mặt phẳng, ta thường sử dụng phương pháp dựng hình hoặc tính toán thông qua các vector pháp tuyến của mặt phẳng. Trong thực tế, khái niệm này được ứng dụng rộng rãi trong kiến trúc, xây dựng và thiết kế công trình, giúp đảm bảo độ chính xác trong việc thi công các kết cấu có góc nghiêng.

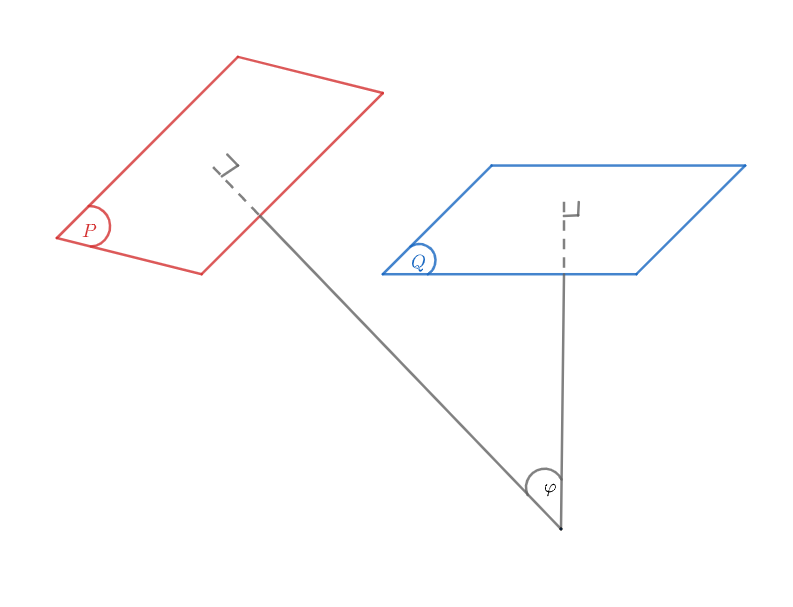
Việc nắm vững cách xác định góc giữa hai mặt phẳng là nền tảng quan trọng để giải quyết nhiều bài toán phức tạp trong hình học không gian, từ tính toán khoảng cách đến xác định vị trí tương đối giữa các đối tượng hình học trong không gian ba chiều.

Phương pháp xác định góc giữa hai mặt phẳng trong không gian

Cách xác định góc giữa hai mặt phẳng được thực hiện thông qua 3 bước chính. Đầu tiên cần xác định giao tuyến của hai mặt phẳng, sau đó dựng mặt phẳng vuông góc với giao tuyến và cuối cùng là tìm góc giữa hai đường thẳng tạo bởi hai mặt phẳng ban đầu.

Để xác định góc giữa hai mặt phẳng một cách chính xác, ta cần áp dụng các kiến thức hình học không gian cơ bản kết hợp với phép chiếu vuông góc. Góc giữa hai mặt phẳng chính là góc nhọn tạo bởi hai đường thẳng vuông góc với giao tuyến của chúng.

Khi cần xác định góc giữa 2 mp, việc thực hiện theo từng bước sẽ giúp bài toán trở nên đơn giản và dễ kiểm soát hơn. Các bước thực hiện được trình bày chi tiết dưới đây.

Xác định giao tuyến của hai mặt phẳng

Bước đầu tiên là tìm giao tuyến của 2 mặt phẳng. Giao tuyến là đường thẳng chung của hai mặt phẳng, được xác định bằng cách giải hệ phương trình của hai mặt phẳng.

Khi hai mặt phẳng cắt nhau, giao tuyến luôn tồn tại và duy nhất. Việc xác định chính xác giao tuyến có ý nghĩa quyết định đến độ chính xác của góc cần tìm.

Xác định mặt phẳng vuông góc với giao tuyến

Sau khi có giao tuyến, ta dựng một mặt phẳng vuông góc với giao tuyến đã tìm được. Mặt phẳng này sẽ cắt hai mặt phẳng ban đầu theo hai đường thẳng.

Mặt phẳng vuông góc với giao tuyến có thể được xác định bằng cách lấy một điểm bất kỳ trên giao tuyến và vector pháp tuyến của nó chính là vector chỉ phương của giao tuyến.

Tìm góc giữa hai đường thẳng tạo bởi hai mặt phẳng

Hai đường thẳng tạo bởi mặt phẳng vuông góc với hai mặt phẳng ban đầu sẽ tạo thành một góc. Góc giữa 2 đường thẳng này chính là góc giữa hai mặt phẳng cần tìm.

Góc này được xác định bằng công thức cosin của góc giữa hai vector chỉ phương của hai đường thẳng. Đây là góc nhọn hoặc góc bẹt tùy thuộc vào vị trí tương đối của hai mặt phẳng ban đầu.

Công thức tính góc giữa hai mặt phẳng và các trường hợp đặc biệt

Góc giữa hai mặt phẳng là một khái niệm quan trọng trong hình học không gian. Để xác định góc giữa hai mặt phẳng, ta cần dựa vào các vector pháp tuyến của chúng. Việc nắm vững công thức tính góc giữa hai mặt phẳng giúp giải quyết nhiều bài toán thực tế trong kiến trúc và xây dựng.

Công thức tổng quát tính góc giữa hai mặt phẳng

Khi hai mặt phẳng cắt nhau, góc giữa chúng được xác định bằng góc giữa hai vector pháp tuyến. Nếu n1(a1,b1,c1) và n2(a2,b2,c2) lần lượt là vector pháp tuyến của hai mặt phẳng, ta có cách tính góc giữa hai mặt phẳng theo công thức:
cos α = |a1a2 + b1b2 + c1c2|/√[(a1² + b1² + c1²)(a2² + b2² + c2²)]

Trong đó α là góc nhọn giữa hai mặt phẳng, luôn nằm trong khoảng từ 0° đến 90°. Dấu giá trị tuyệt đối trong tử số đảm bảo ta luôn nhận được góc nhọn giữa hai mặt phẳng.

Trường hợp hai mặt phẳng vuông góc

Hai mặt phẳng vuông góc khi và chỉ khi các vector pháp tuyến của chúng vuông góc với nhau. Điều này xảy ra khi tích vô hướng của hai vector pháp tuyến bằng 0:
a1a2 + b1b2 + c1c2 = 0

Khi đó góc giữa hai mặt phẳng sẽ bằng 90°. Đây là trường hợp đặc biệt thường gặp trong các công trình xây dựng, như góc giữa tường và sàn nhà.

Trường hợp hai mặt phẳng song song

Khi góc giữa 2 mp bằng 0°, hai mặt phẳng song song với nhau. Trong trường hợp này, các vector pháp tuyến của hai mặt phẳng cùng phương hoặc ngược phương. chứng minh hai mặt phẳng song song

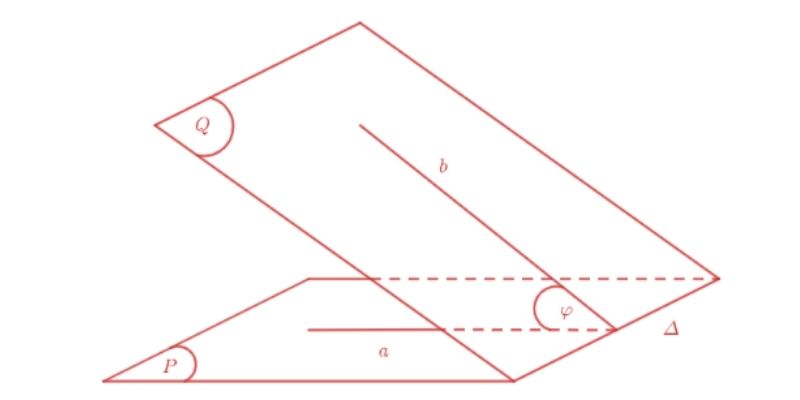
Vector pháp tuyến của mặt phẳng thứ nhất sẽ là một số k ≠ 0 nhân với vector pháp tuyến của mặt phẳng thứ hai:
n1 = k.n2 hay (a1,b1,c1) = k(a2,b2,c2)

Điều này dẫn đến các tỉ số: a1/a2 = b1/b2 = c1/c2 = k, là điều kiện cần và đủ để hai mặt phẳng song song.

Các bài toán thường gặp về góc giữa hai mặt phẳng

Trong hình học không gian, việc tìm góc giữa hai mặt phẳng là một dạng bài toán quan trọng và phổ biến. Để giải quyết các bài toán này hiệu quả, cần nắm vững phương pháp xác định góc giữa hai mặt phẳng thông qua góc giữa hai đường thẳng vuông góc với giao tuyến của chúng. Dạy toán trực tuyến sẽ giúp bạn hiểu rõ hơn về các dạng bài tập cơ bản.

Bài toán về góc giữa mặt phẳng và mặt đáy của hình chóp

Khi xác định góc giữa mặt phẳng và mặt đáy của hình chóp, ta thường sử dụng phương pháp dựng đường vuông góc từ đỉnh chóp xuống mặt đáy. Góc tạo bởi đường vuông góc này với mặt phẳng cần tìm chính là góc phụ của góc giữa hai mặt phẳng.

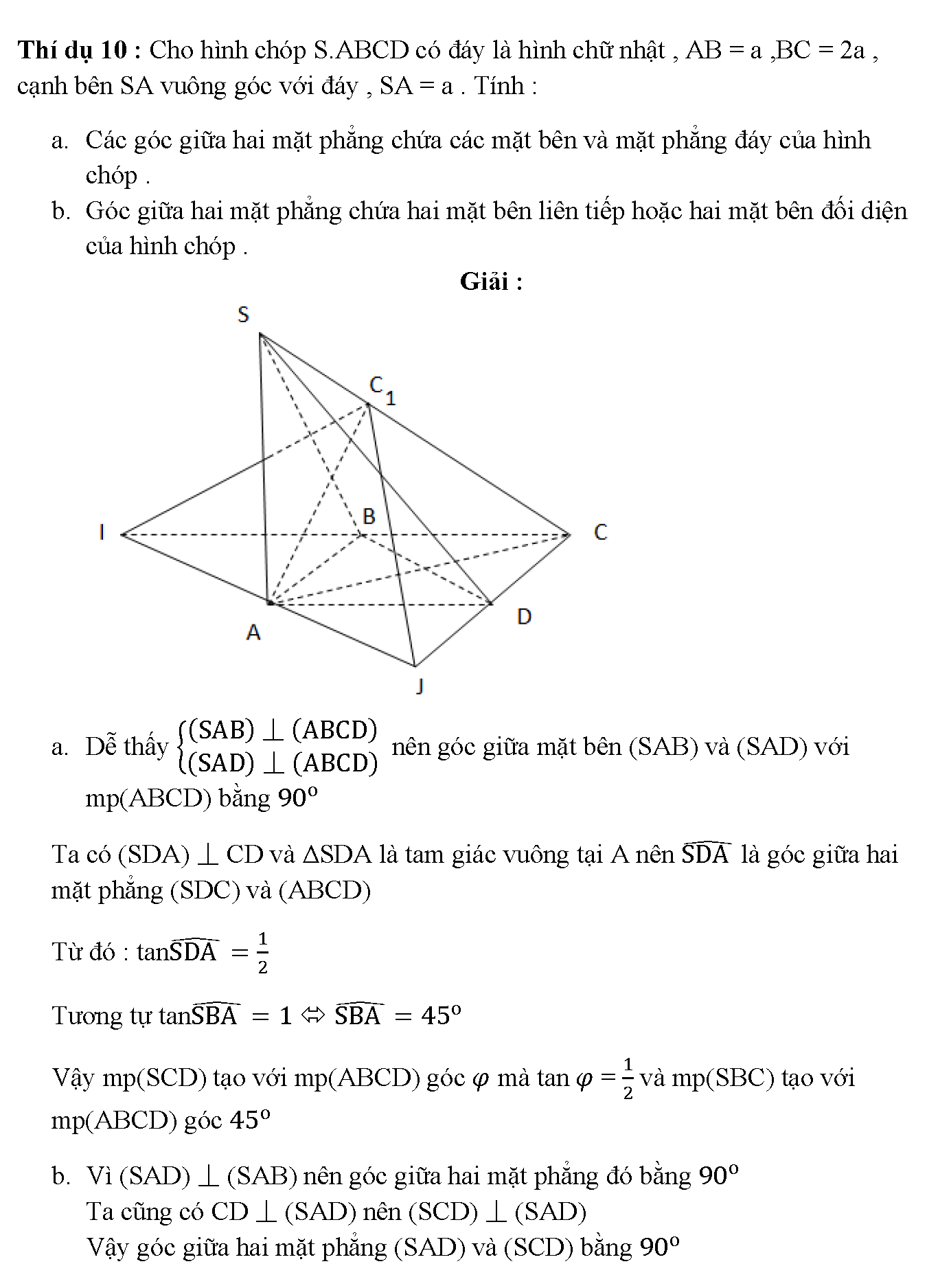
Một cách tiếp cận khác là sử dụng phép chiếu vuông góc của các cạnh bên lên mặt đáy. Phương pháp này đặc biệt hiệu quả khi hình chóp có tính đối xứng hoặc các cạnh bên bằng nhau.

Bài toán về góc giữa hai mặt bên của hình chóp

Để xác định góc tạo bởi 2 mặt phẳng bên của hình chóp, ta cần xác định giao tuyến của hai mặt phẳng – chính là cạnh bên chung của chúng. Sau đó, dựng hai đường vuông góc với giao tuyến, mỗi đường nằm trên một mặt phẳng.

Góc giữa hai đường vuông góc này chính là góc giữa hai mặt phẳng. Trong trường hợp hình chóp đều, góc này có thể tính được thông qua các yếu tố đã biết như chiều cao, cạnh đáy và cạnh bên.

Bài toán về góc giữa hai mặt phẳng trong hình lăng trụ

Trong hình lăng trụ, góc giữa hai mặt phẳng thường xuất hiện dưới hai dạng: góc giữa mặt bên và mặt đáy, hoặc góc giữa hai mặt bên. Với mặt bên và mặt đáy, góc giữa chúng luôn là 90 độ do tính chất của hình lăng trụ.

Đối với góc giữa hai mặt bên, ta cần xác định giao tuyến của chúng (cạnh bên chung) và áp dụng định lý về góc giữa hai mặt phẳng. Việc tính toán thường đơn giản hơn so với hình chóp do tính song song của các cạnh bên.

Phương pháp giải nhanh các dạng bài tập về góc giữa hai mặt phẳng

Để giải quyết các bài toán về góc giữa hai mặt phẳng trong không gian, việc nắm vững phương pháp và kỹ thuật giải nhanh là rất quan trọng. Góc giữa hai mặt phẳng được xác định thông qua góc giữa 2 vecto pháp tuyến của chúng.

Khi xác định cách tìm góc giữa 2 mặt phẳng, ta cần phân tích kỹ các yếu tố hình học và áp dụng các công thức phù hợp. Việc này giúp rút ngắn thời gian giải và tăng độ chính xác của kết quả.

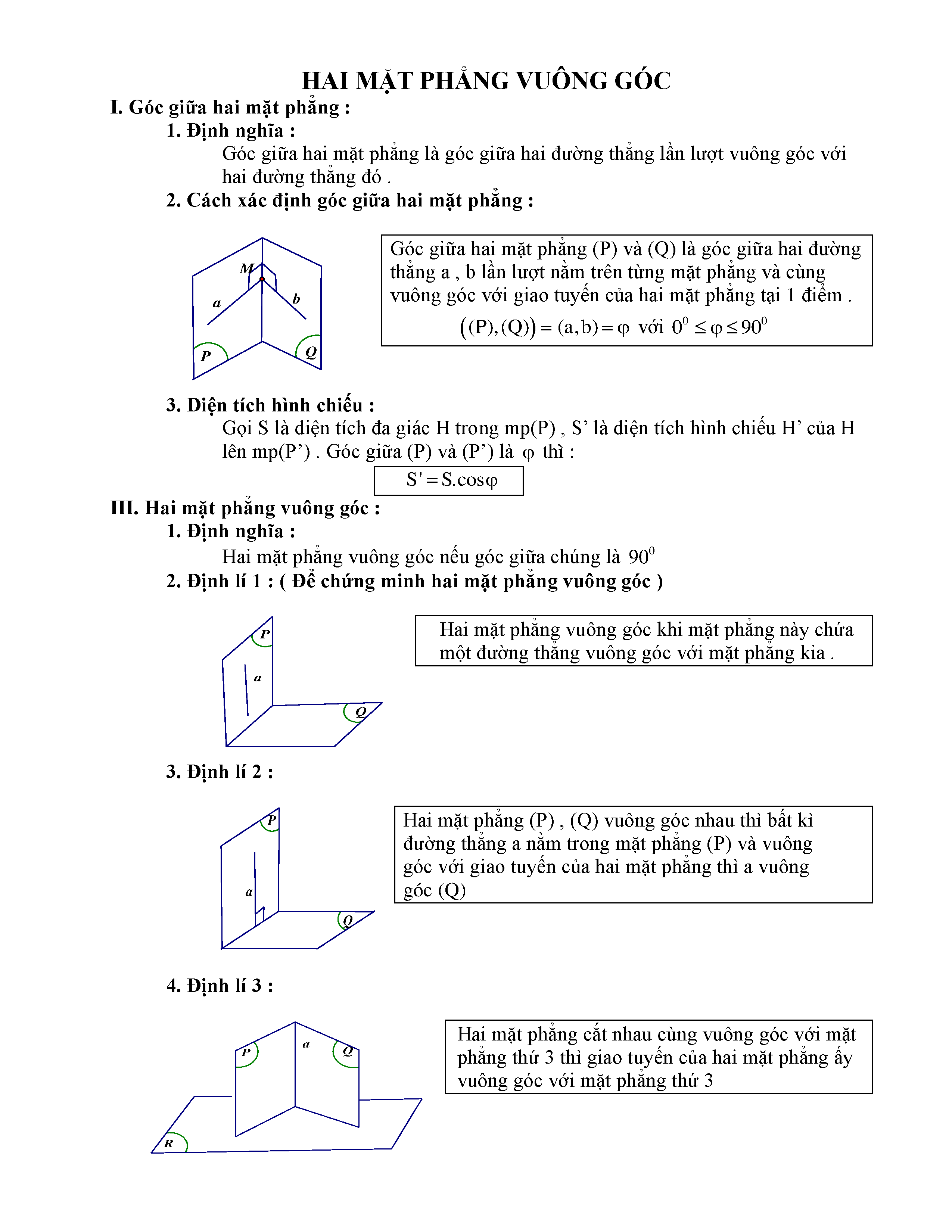
Nhận dạng các dạng bài tập điển hình

Dạng 1: Tìm góc giữa hai mặt phẳng khi biết phương trình của chúng. Với dạng này, ta cần xác định vecto pháp tuyến từ hệ số của phương trình mặt phẳng.

Dạng 2: Tìm góc giữa hai mặt phẳng khi biết các điểm xác định mặt phẳng. Trường hợp này đòi hỏi tính toán vecto pháp tuyến thông qua tích có hướng của các vecto.

Dạng 3: Bài toán về hai góc phụ nhau giữa hai mặt phẳng, thường gặp trong các bài toán phức tạp về hình học không gian.

Các mẹo giải nhanh

Khi giải bài toán góc giữa hai mặt phẳng, việc đầu tiên là xác định vecto pháp tuyến của từng mặt phẳng. Nếu phương trình mặt phẳng có dạng ax + by + cz + d = 0, vecto pháp tuyến sẽ là n(a,b,c).

Công thức tính góc giữa hai mặt phẳng:
cos α = |n1.n2|/(|n1|.|n2|)
Trong đó n1, n2 là các vecto pháp tuyến của hai mặt phẳng.

Với các bài toán có nhiều mặt phẳng, nên vẽ hình phụ để hình dung rõ mối quan hệ không gian giữa chúng.

Lưu ý khi giải bài tập

Cần kiểm tra kỹ dữ kiện bài toán và điều kiện của các mặt phẳng. Một số mặt phẳng có thể song song hoặc vuông góc, làm đơn giản hóa việc tính toán.

Khi tính góc giữa hai mặt phẳng, luôn lấy góc nhỏ nhất giữa chúng. Nếu kết quả tính được là góc lớn, cần lấy góc phụ của nó.

Đối với bài toán phức tạp, nên chia nhỏ thành các bước giải quyết riêng biệt: xác định vecto pháp tuyến, chuẩn hóa vecto, áp dụng công thức tính góc.

Góc giữa 2 mặt phẳng là một khái niệm cơ bản và quan trọng trong hình học không gian. Hiểu rõ cách xác định và tính toán góc giữa hai mặt phẳng sẽ giúp học sinh áp dụng vào các bài toán thực tiễn hiệu quả hơn. Bằng cách nắm vững công thức và phương pháp giải, các bạn sẽ tự tin hơn khi đối diện với các bài tập liên quan đến vấn đề này.