Tìm hiểu tứ giác nội tiếp là gì và các tính chất, bài tập ứng dụng trong hình học

Tứ giác nội tiếp là gì? Đây là một khái niệm quan trọng trong hình học, đặc biệt trong nghiên cứu về tứ giác và đường tròn. Bài viết này sẽ trình bày các tính chất, phương pháp chứng minh và ứng dụng thực tiễn của tứ giác nội tiếp, giúp bạn hiểu rõ hơn về dạng hình học đặc biệt này.

Tứ giác nội tiếp là gì?

Tứ giác nội tiếp là gì – đây là một khái niệm hình học chỉ tứ giác có tất cả 4 đỉnh nằm trên cùng một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp của tứ giác. Để một tứ giác lồi trở thành tứ giác nội tiếp đường tròn, nó cần thỏa mãn một số tính chất đặc biệt.

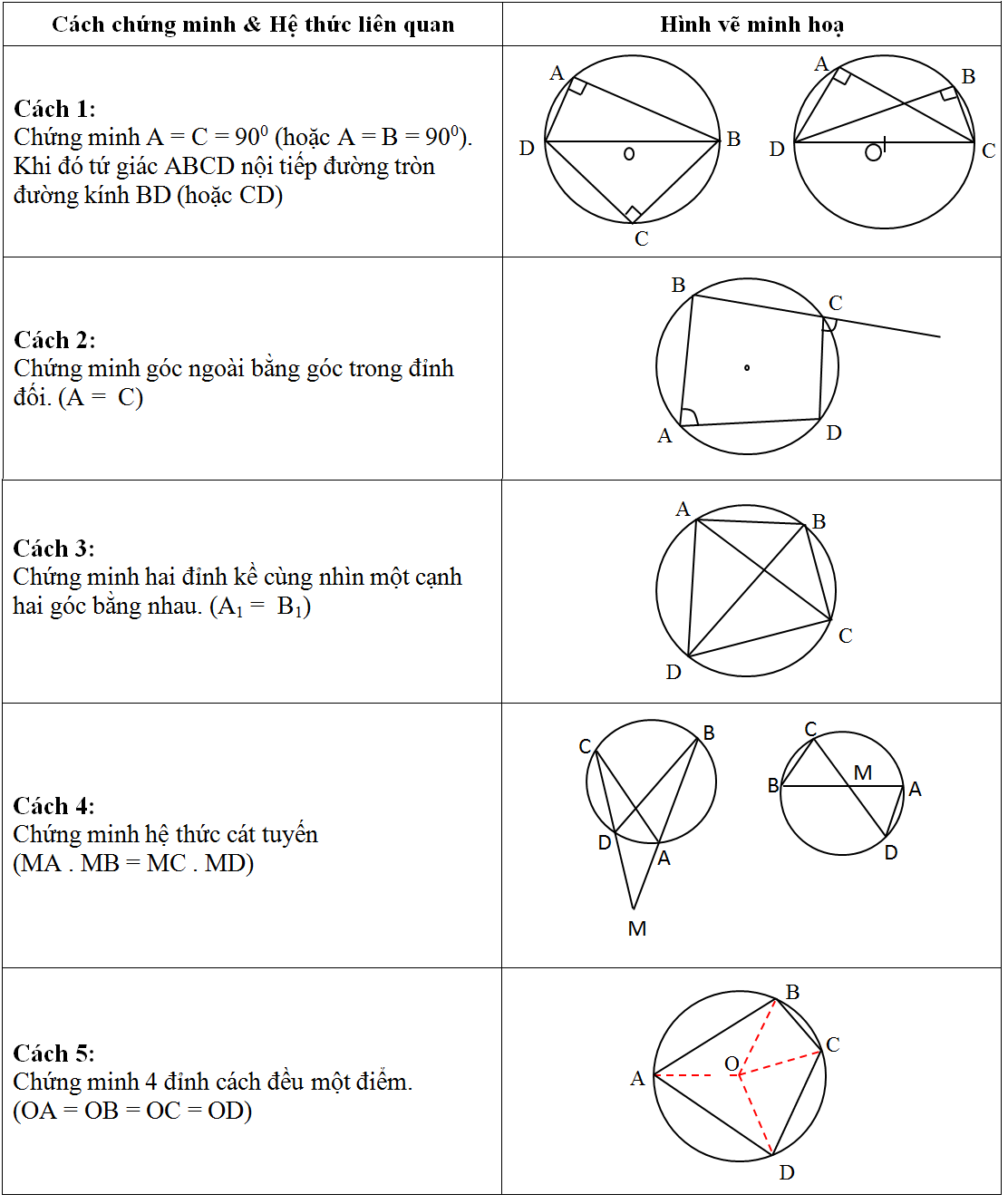
Một tứ giác có thể nội tiếp được trong đường tròn khi và chỉ khi tổng các góc đối bằng 180 độ. Điều này có nghĩa là nếu gọi các góc của tứ giác lần lượt là A, B, C, D thì A + C = B + D = 180°. Đây là điều kiện cần và đủ để xác định một tứ giác có thể nội tiếp được trong đường tròn hay không.

Trong thực tế, tứ giác nội tiếp xuất hiện phổ biến trong kiến trúc và thiết kế. Ví dụ như các mái vòm trong kiến trúc Gothic thường được thiết kế dựa trên nguyên lý của tứ giác nội tiếp, tạo nên những đường cong hài hòa và cân đối. Tương tự, trong thiết kế logo, các designer thường sử dụng tứ giác nội tiếp để tạo ra những hình ảnh có tính thẩm mỹ cao và cân đối về mặt hình học.

Các tính chất quan trọng của tứ giác nội tiếp đường tròn

Tính chất tứ giác nội tiếp là những đặc điểm đặc trưng giúp phân biệt loại tứ giác này với các tứ giác thông thường khác. Những tính chất này không chỉ giúp chứng minh các bài toán hình học mà còn có ứng dụng thực tiễn trong thiết kế và xây dựng.

Để hiểu rõ hơn về các tính chất này, ta cần xem xét từng khía cạnh cụ thể liên quan đến góc, cạnh và các yếu tố hình học khác. Tính chất của tứ giác nội tiếp được áp dụng rộng rãi trong việc giải các bài toán phức tạp.

Tính chất về các góc đối của tứ giác nội tiếp

Trong một tứ giác nội tiếp, tổng số đo của hai góc đối bằng 180°. Đây là một trong những tính chất tứ giác nội tiếp lớp 9 cơ bản nhất mà học sinh cần nắm vững.

Tính chất này có mối liên hệ chặt chẽ với đường tròn nội tiếp tam giác, bởi khi chia tứ giác nội tiếp thành hai tam giác bằng đường chéo, ta có thể áp dụng các tính chất của đường tròn nội tiếp tam giác.

Tính chất về các cạnh và đường chéo

Trong tứ giác nội tiếp, tích của các đoạn mà một đường chéo chia đường chéo kia bằng nhau. Điều này tạo nên mối quan hệ đặc biệt giữa các phần của đường chéo.

Ngoài ra, tích của các đoạn thẳng được tạo bởi một điểm bất kỳ trên đường tròn đến hai đầu mút của một cạnh luôn bằng tích của các đoạn thẳng từ điểm đó đến hai đầu mút của cạnh đối diện.

Mối quan hệ giữa bán kính đường tròn và các yếu tố của tứ giác

Bán kính đường tròn ngoại tiếp của tứ giác có thể được tính thông qua diện tích tứ giác và độ dài các cạnh. Công thức này được biết đến với tên gọi công thức Euler.

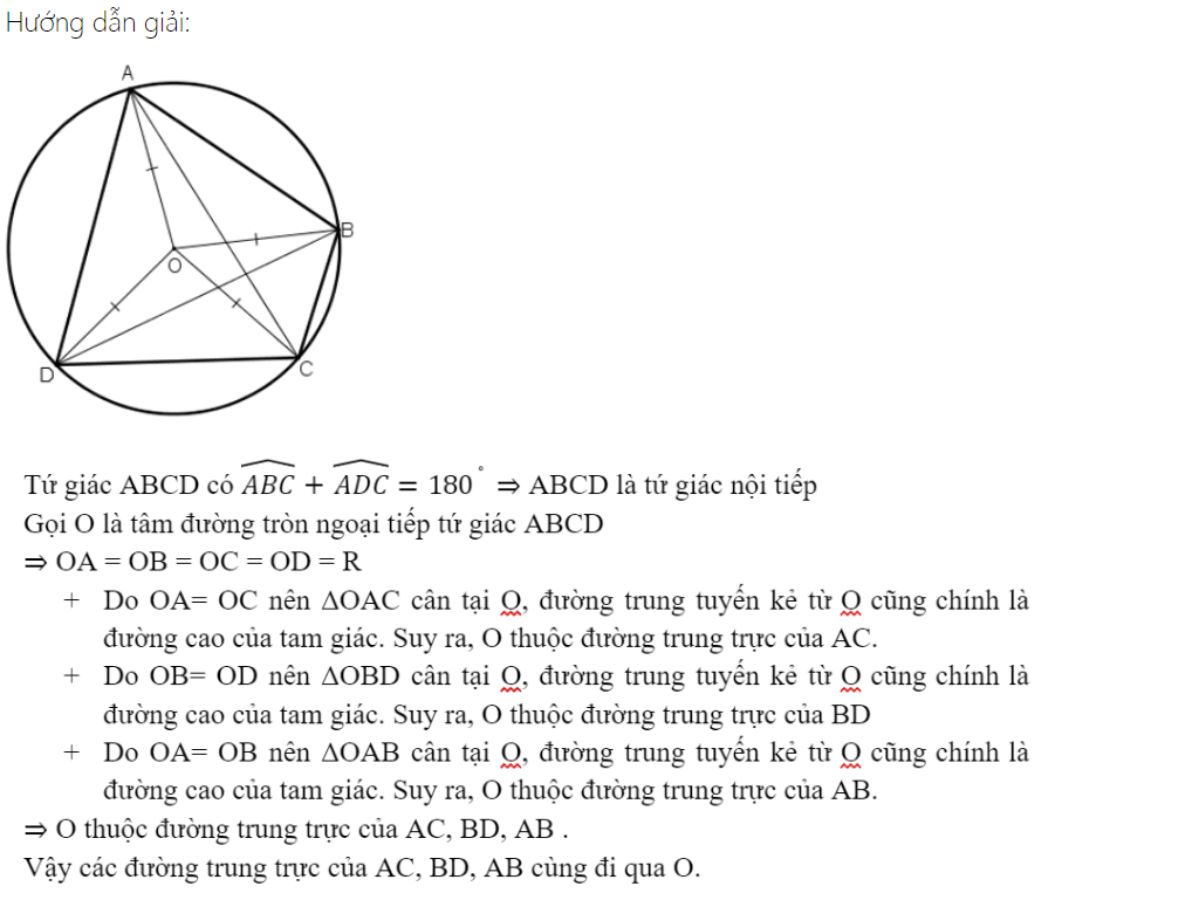
Mối quan hệ này còn thể hiện qua tỷ số giữa diện tích tứ giác và tích của các cạnh. Đây là một công cụ hữu ích trong việc tính toán các yếu tố chưa biết của tứ giác nội tiếp khi có đủ dữ kiện.

Phương pháp chứng minh một tứ giác là tứ giác nội tiếp

Để chứng minh một tứ giác là tứ giác nội tiếp, ta cần xác định được các điều kiện cần và đủ. Định lý tứ giác nội tiếp cho thấy một tứ giác có thể nội tiếp được trong đường tròn khi và chỉ khi tổng các góc đối bằng 180°. Việc chứng minh có thể thực hiện thông qua nhiều phương pháp khác nhau, tùy thuộc vào dữ kiện đã cho.

Khi nghiên cứu về tứ giác nội tiếp suy ra được gì, ta thấy rằng từ tính chất này có thể suy ra nhiều kết quả quan trọng như tính chất góc nội tiếp, tính chất đường cao, tính chất đường trung tuyến. Những tính chất này có mối liên hệ chặt chẽ với miền nghiệm của bất phương trình trong nhiều bài toán hình học.

Sử dụng tính chất góc nội tiếp

Phương pháp sử dụng tính chất góc nội tiếp là một trong những cách phổ biến nhất để cách chứng minh tứ giác nội tiếp. Khi hai góc nội tiếp cùng chắn một cung thì bằng nhau, và góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung.

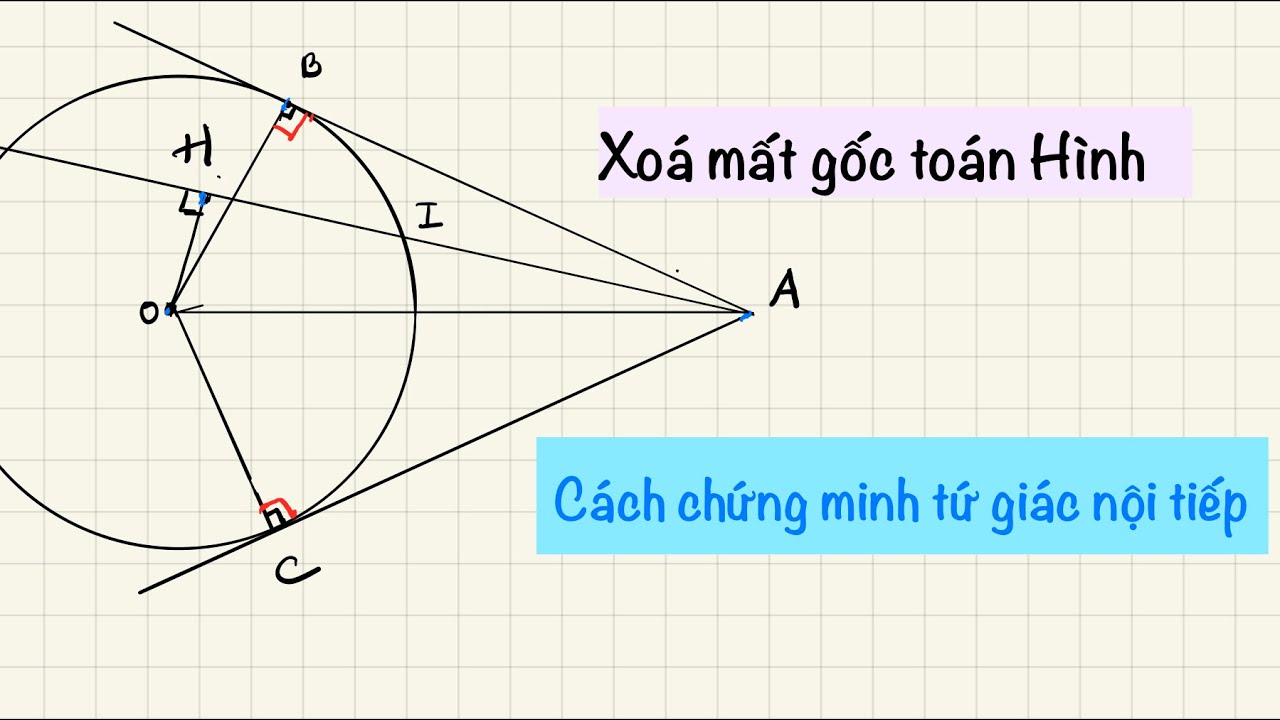
Việc áp dụng tính chất này đòi hỏi sự phân tích kỹ lưỡng các góc trong tứ giác. Thông thường, ta sẽ tìm các cặp góc bằng nhau hoặc các góc có quan hệ với nhau thông qua các cung chung.

Sử dụng định lý về tứ giác nội tiếp

Định lý về tứ giác nội tiếp cung cấp một công cụ mạnh mẽ để chứng minh. Nếu tổng hai góc đối của tứ giác bằng 180°, tứ giác đó chắc chắn nội tiếp được trong một đường tròn.

Khi áp dụng định lý này, ta cần chú ý đến việc chứng minh tổng các góc đối. Có thể sử dụng các phép biến đổi đại số, các tính chất của tam giác, hoặc các quan hệ góc để thiết lập điều này.

Các trường hợp đặc biệt

Một số trường hợp đặc biệt của tứ giác nội tiếp cần được xem xét riêng. Hình chữ nhật luôn là tứ giác nội tiếp vì có tất cả các góc bằng 90°. Hình thang cân cũng là tứ giác nội tiếp do tính đối xứng của nó.

Trong thực tế, việc nhận biết các trường hợp đặc biệt giúp rút ngắn quá trình chứng minh đáng kể. Thay vì phải chứng minh từ định nghĩa, ta có thể sử dụng các tính chất riêng của từng loại tứ giác.

Các dạng bài tập thường gặp về tứ giác nội tiếp

Khi học về hình học phẳng, tứ giác nội tiếp là gì luôn là câu hỏi được nhiều học sinh quan tâm. Đây là dạng bài tập quan trọng thường xuất hiện trong các đề thi và kiểm tra. Để giúp các bạn nắm vững kiến thức, Hãy cùng tìm hiểu các dạng bài tập về tứ giác nội tiếp.

Bài tập chứng minh tứ giác nội tiếp

Dạng bài tập chứng minh tứ giác nội tiếp thường yêu cầu học sinh vận dụng các tính chất đặc trưng để chứng minh một tứ giác cho trước là tứ giác nội tiếp. Phương pháp chứng minh phổ biến là sử dụng định lý về tổng các góc đối, định lý về tích các đoạn thẳng.

Một số ví dụ về tứ giác nội tiếp điển hình là chứng minh tứ giác ABCD nội tiếp đường tròn khi biết hai góc đối bằng nhau hoặc tổng hai góc đối bằng 180°. Việc nắm vững các tính chất và định lý sẽ giúp giải quyết dễ dàng các bài toán này.

Bài tập tính toán các yếu tố của tứ giác nội tiếp

Trong các bài tập tứ giác nội tiếp, dạng tính toán các yếu tố như độ dài cạnh, số đo góc, diện tích thường xuyên xuất hiện. Việc áp dụng các công thức về tỉ số độ dài đoạn thẳng, định lý sin trong tam giác là chìa khóa giải quyết.

Khi giải các bài toán này, cần xác định rõ các yếu tố đã biết và cần tìm, sau đó vận dụng linh hoạt các công thức và tính chất để tìm ra kết quả. Đặc biệt chú ý đến mối liên hệ giữa các góc và cạnh trong tứ giác nội tiếp.

Bài tập ứng dụng tính chất tứ giác nội tiếp

Các bài toán ứng dụng tính chất tứ giác nội tiếp thường đòi hỏi sự kết hợp nhiều kiến thức và kỹ năng. Từ việc nhận biết tứ giác nội tiếp qua các điều kiện cho trước đến việc vận dụng các tính chất để giải quyết bài toán phức tạp hơn.

Một số ứng dụng thực tế của tứ giác nội tiếp có thể thấy trong kiến trúc và xây dựng, như thiết kế mái vòm hay cổng chào. Các kiến trúc sư thường áp dụng tính chất của tứ giác nội tiếp để tạo ra những công trình vừa đẹp vừa vững chắc.

Việc thực hành nhiều dạng bài tập khác nhau sẽ giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề trong hình học. Mỗi dạng bài tập đều có những đặc thù riêng và cách tiếp cận phù hợp.

Ứng dụng của tứ giác nội tiếp trong thực tế và các bài toán hình học

Tứ giác nội tiếp là gì – một hình học phẳng có 4 đỉnh nằm trên cùng một đường tròn. Đây là một khái niệm toán học quan trọng với nhiều ứng dụng tứ giác nội tiếp thực tiễn. Các công thức tứ giác nội tiếp giúp giải quyết nhiều bài toán phức tạp trong xây dựng, thiết kế và nghệ thuật. Việc áp dụng tính chất đặc biệt của loại tứ giác này mang lại hiệu quả cao trong nhiều lĩnh vực.

Ứng dụng trong xây dựng và kiến trúc

Trong lĩnh vực xây dựng, tứ giác nội tiếp được ứng dụng rộng rãi để thiết kế mái vòm và các cấu trúc cong. Theo kiến trúc sư Frank Gehry, việc sử dụng nguyên lý tứ giác nội tiếp giúp tạo ra những đường cong mềm mại nhưng vẫn đảm bảo độ vững chắc cho công trình.

Các công trình như nhà thờ Sagrada Familia ở Barcelona áp dụng tính chất của tứ giác nội tiếp để thiết kế hệ thống mái vòm phức tạp. Điều này không chỉ tạo nên vẻ đẹp thẩm mỹ mà còn đảm bảo tính ổn định về mặt kỹ thuật cho toàn bộ công trình.

Ứng dụng trong thiết kế và mỹ thuật

Trong nghệ thuật tạo hình, tứ giác nội tiếp đóng vai trò quan trọng trong việc tạo ra các mẫu hình học và họa tiết trang trí. Các nghệ sĩ thường sử dụng nguyên lý này để vẽ các hoa văn Islamic truyền thống, tạo nên những tác phẩm nghệ thuật độc đáo và tinh tế.

Nhà thiết kế nổi tiếng Philippe Starck thường xuyên áp dụng tính chất của tứ giác nội tiếp trong thiết kế nội thất. Ông cho rằng việc sử dụng các đường cong hài hòa dựa trên nguyên lý này giúp tạo ra không gian sống thoải mái và thân thiện hơn với người sử dụng.

Trong thiết kế logo và nhận diện thương hiệu, nhiều công ty cũng áp dụng nguyên lý tứ giác nội tiếp để tạo ra biểu tượng cân đối và bắt mắt.

Ứng dụng trong các bài toán tổng hợp

Tứ giác nội tiếp được sử dụng để giải quyết nhiều bài toán phức tạp trong hình học. Ví dụ như bài toán tìm diện tích tứ giác khi biết 4 cạnh, hay xác định góc của tứ giác khi biết một số yếu tố.

Trong lĩnh vực robot học, các kỹ sư tại MIT đã ứng dụng tính chất của tứ giác nội tiếp để thiết kế cơ cấu chuyển động cho robot. Điều này giúp robot có thể thực hiện các chuyển động mượt mà và chính xác hơn.

Ngoài ra, trong quy hoạch đô thị, các kiến trúc sư sử dụng nguyên lý tứ giác nội tiếp để thiết kế hệ thống giao thông và không gian công cộng, tạo ra môi trường sống hài hòa và thuận tiện cho người dân.

Tứ giác nội tiếp là một khái niệm quan trọng trong hình học, giúp học sinh hiểu rõ hơn về những tính chất độc đáo của các tứ giác. Bài viết đã trình bày các tính chất của tứ giác nội tiếp, phương pháp chứng minh và ứng dụng trong thực tế, các bài tập liên quan. Nắm vững tứ giác nội tiếp là gì sẽ giúp các em áp dụng kiến thức vào giải quyết các bài toán phức tạp hơn trong môn hình học. Hãy tiếp tục tìm hiểu và thực hành để củng cố kiến thức này.